Triangles - Trigonometry
Card 1 of 644
You need to build a diagonal support for the bleachers at the local sportsfield. The support needs to reach from the ground to the top of the bleacher. How the support should look is highlighted in blue below. The bleacher wall is 10 feet high and perpendicular to the ground. The owner would like the support to only stick out 3 feet from the bleacher at the bottom. What is the length of the support you need to build?
You need to build a diagonal support for the bleachers at the local sportsfield. The support needs to reach from the ground to the top of the bleacher. How the support should look is highlighted in blue below. The bleacher wall is 10 feet high and perpendicular to the ground. The owner would like the support to only stick out 3 feet from the bleacher at the bottom. What is the length of the support you need to build?
Tap to reveal answer
It is important to recognize that the bleacher, the ground, and the support form a right triangle with the right angle formed by the intersection of the bleacher wall and the ground. We know the bottom of the support should only be 3ft from the bleacher wall on the ground and the bleacher wall is 10ft high. We will use the Pythagorean Theorem to solve for the length of the support, which is the hypotenuse of this right triangle. Our base of the triangle is 3 feet and the leg is 10 feet.
And so we need a support of 10.44 feet long.
It is important to recognize that the bleacher, the ground, and the support form a right triangle with the right angle formed by the intersection of the bleacher wall and the ground. We know the bottom of the support should only be 3ft from the bleacher wall on the ground and the bleacher wall is 10ft high. We will use the Pythagorean Theorem to solve for the length of the support, which is the hypotenuse of this right triangle. Our base of the triangle is 3 feet and the leg is 10 feet.
And so we need a support of 10.44 feet long.
← Didn't Know|Knew It →
An airplane takes off from point 
and reaches its maximum altitude of 31,000 ft. The angle from the point of takeoff to the plane at maximum altitude is 55 degrees. What is the distance from point 
to where the plane reaches maximum altitude?
An airplane takes off from point 
Tap to reveal answer
We begin by drawing a picture. Let 
stand for where the plane reaches a maximum altitude of 31,000 ft. We can also assume that if we draw a line straight down from the plane that it will be perpendicular to the ground. This forms a right triangle.
Now we will use our knowledge of right triangles. We know the trigonometric identity, 
. We can plug 55 in for our 
and 31,000 in for the opposite side. Solving for the hypotenuse is solving for the distance from the point of takeoff to the plane when it reaches maximum altitude.
And so the distance from point 
to the plane at maximum altitude is 37,844 ft.
We begin by drawing a picture. Let 
Now we will use our knowledge of right triangles. We know the trigonometric identity, 
And so the distance from point 
← Didn't Know|Knew It →
You are reading a billboard perpendicular to the ground walking downtown. You are standing about 500 ft from the base of the billboard and looking up at an angle of 67 degrees. About what height is the part of the billboard you are looking at standing at? Round to the nearest whole number.
You are reading a billboard perpendicular to the ground walking downtown. You are standing about 500 ft from the base of the billboard and looking up at an angle of 67 degrees. About what height is the part of the billboard you are looking at standing at? Round to the nearest whole number.
Tap to reveal answer
We begin by drawing a picture. Let point 
be where your eyes are looking on the billboard and point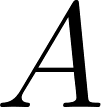 
be where you are standing on the ground.
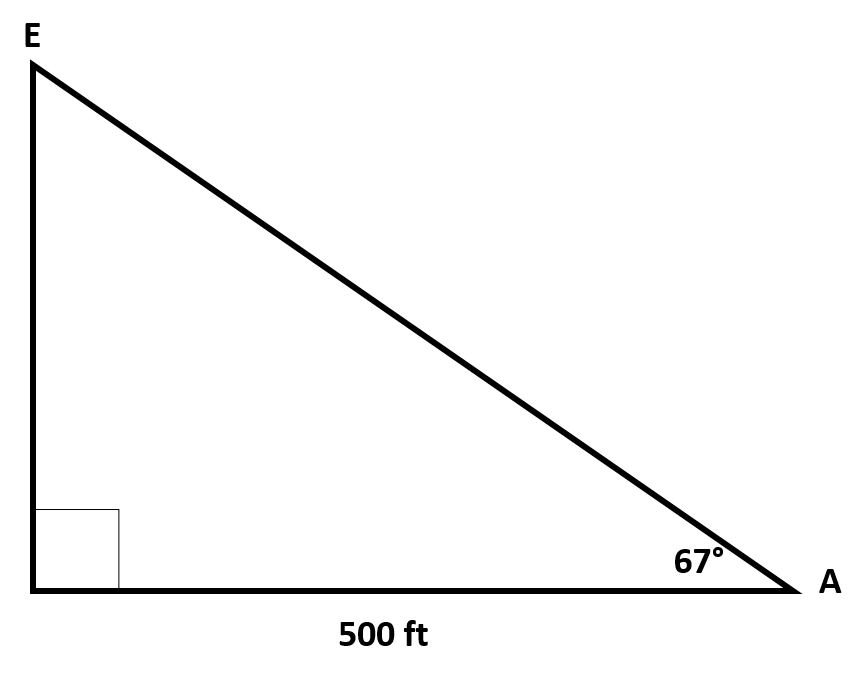
We must solve for the height of the billboard. We have information of the adjacent side of the right triangle formed and we wish to know the height, which will be the opposite side from you. Using trigonometric identities, we will use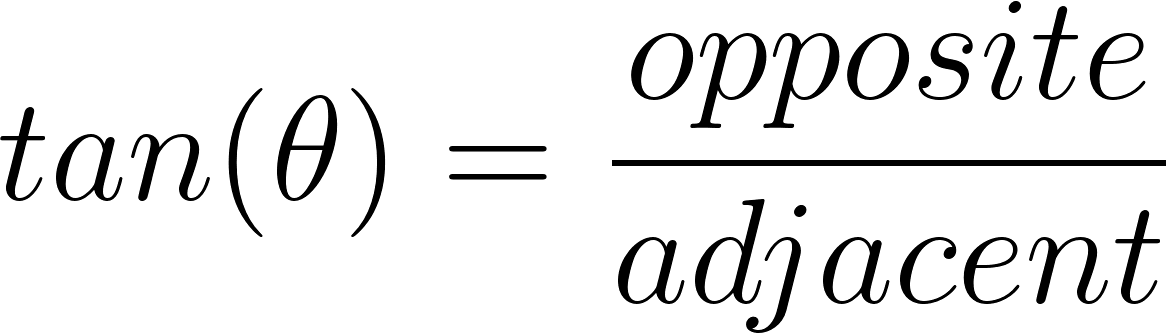 
. We can plug in 500 ft for our adjacent side and 67 degrees for our 
.
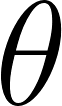And the height of the section of the billboard you are looking at is 1,178 ft above the ground.
We begin by drawing a picture. Let point
We must solve for the height of the billboard. We have information of the adjacent side of the right triangle formed and we wish to know the height, which will be the opposite side from you. Using trigonometric identities, we will use
And the height of the section of the billboard you are looking at is 1,178 ft above the ground.
← Didn't Know|Knew It →
You have a shadow that measures 66cm from your feet. You are 60cm tall. What is the sun’s angle of elevation? Round to the nearest degree.
You have a shadow that measures 66cm from your feet. You are 60cm tall. What is the sun’s angle of elevation? Round to the nearest degree.
Tap to reveal answer
The important thing to note for this problem is that we are working with similar triangles. Your shadow forms a right triangle with its three points being your feet, the top of your head, and the top of your shadow’s head. We have enough information to find the angle of your head’s elevation to your shadow on the ground. Just like your shadow forms a right triangle to your body, a similar right triangle will also be formed to the sun’s altitude. We know that this triangle is similar because it shares the angle opposite your body and it shares a right angle, so it’s third angle must also be equal. Since it shares the angle opposite your body, we must only solve for the angle of your head’s elevation and it will be the same as the sun’s elevation.
We do this by using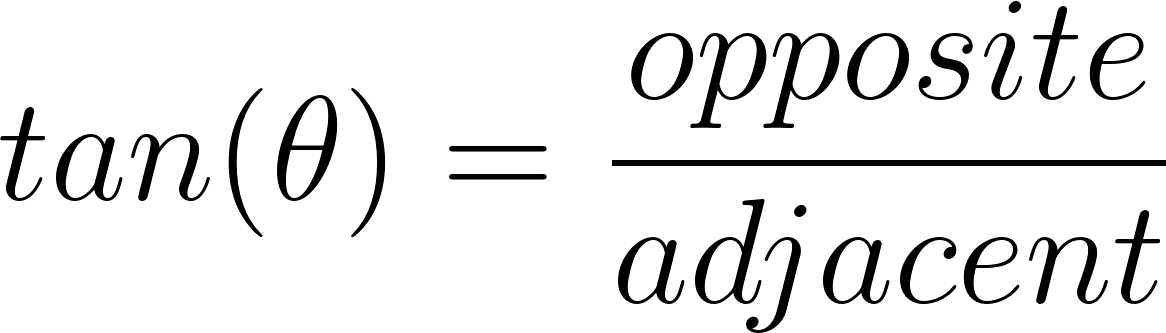 
. We can plug in 60cm for the opposite since that is your height, and 66cm for the adjacent since that is the length of the shadow. We are solving for 
.
And so the sun is at an elevation of 48 degrees.
The important thing to note for this problem is that we are working with similar triangles. Your shadow forms a right triangle with its three points being your feet, the top of your head, and the top of your shadow’s head. We have enough information to find the angle of your head’s elevation to your shadow on the ground. Just like your shadow forms a right triangle to your body, a similar right triangle will also be formed to the sun’s altitude. We know that this triangle is similar because it shares the angle opposite your body and it shares a right angle, so it’s third angle must also be equal. Since it shares the angle opposite your body, we must only solve for the angle of your head’s elevation and it will be the same as the sun’s elevation.
We do this by using
And so the sun is at an elevation of 48 degrees.
← Didn't Know|Knew It →
Given the accompanying right triangle where 
and 
, determine the measure of 
to the nearest degree.
Given the accompanying right triangle where
Tap to reveal answer
We are given two sides of the right triangle, namely the hypotenuse and the opposite side of the angle. Therefore, we simply use the sine function to determine the angle:
In order to isolate the angle we must apply the inverse sine function to both sides:
We are given two sides of the right triangle, namely the hypotenuse and the opposite side of the angle. Therefore, we simply use the sine function to determine the angle:
In order to isolate the angle we must apply the inverse sine function to both sides:
← Didn't Know|Knew It →
Given a right triangle where 
, find the missing side.
Given a right triangle where
Tap to reveal answer
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are given. Since the function we are given is sine, we know that we are given the opposite side and the hypotenuse. Therefore, setting up the equation:
Where, 
and 
are given.
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are given. Since the function we are given is sine, we know that we are given the opposite side and the hypotenuse. Therefore, setting up the equation:
Where,
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
← Didn't Know|Knew It →
Given a right triangle where 
, find the missing side.
Given a right triangle where
Tap to reveal answer
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are give. Since the function we are given is tangent, we know that we are given the opposite and adjacent sides. Therefore, setting up the equation:
Where, 
and 
are given.
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are give. Since the function we are given is tangent, we know that we are given the opposite and adjacent sides. Therefore, setting up the equation:
Where,
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
← Didn't Know|Knew It →
Given a right triangle where 
, find the missing side.
Given a right triangle where
Tap to reveal answer
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are given. Since the function we are given is cosine, we know that we are given the adjacent side and hypotenuse. Therefore, setting up the equation:
Where, 
and 
are given.
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
Since the triangle in question is a right triangle we can use the Pythagorean Theorem. First, we must determine which sides we are given. Since the function we are given is cosine, we know that we are given the adjacent side and hypotenuse. Therefore, setting up the equation:
Where,
Solving the above equation:
We toss out the negative solution since the length of a side must be positive.
← Didn't Know|Knew It →
A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25o angle with the ground. How long is the wire, w? Round your answer to two decimal places.
A support wire is anchored 10 meters up from the base of a flagpole, and the wire makes a 25o angle with the ground. How long is the wire, w? Round your answer to two decimal places.
Tap to reveal answer
To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25o, the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w.
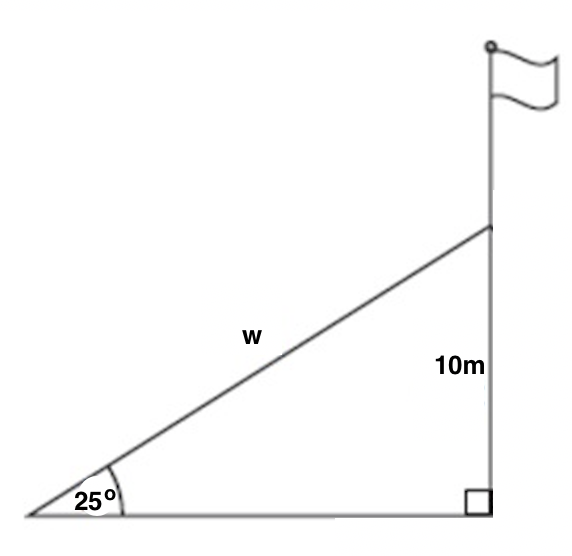
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25o. 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.
We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:
(Use a calculator in degree mode to find that 
after rounding to two decimal places)
meters
To solve this problem instead using the cosecant function, we would get:
(Use a calculator in degree mode to find that 
after rounding to two decimal places)
meters
The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem.
Please note that the answer choice 
is correct based on the Pythagorean Theorem, but does not use all of the provided info to find an exact solution rounded to two decimal places.
To make sense of the problem, start by drawing a diagram. Label the angle of elevation as 25o, the height between the ground and where the wire hits the flagpole as 10 meters, and our unknown, the length of the wire, as w.
Now, we just need to solve for w using the information given in the diagram. We need to ask ourselves which parts of a triangle 10 and w are relative to our known angle of 25o. 10 is opposite this angle, and w is the hypotenuse. Now, ask yourself which trig function(s) relate opposite and hypotenuse. There are two correct options: sine and cosecant. Using sine is probably the most common, but both options are detailed below.
We know that sine of a given angle is equal to the opposite divided by the hypotenuse, and cosecant of an angle is equal to the hypotenuse divided by the opposite (just the reciprocal of the sine function). Therefore:
To solve this problem instead using the cosecant function, we would get:
The reason that we got 23.7 here and 23.81 above is due to differences in rounding in the middle of the problem.
Please note that the answer choice 
← Didn't Know|Knew It →
Which of the following is true about the right triangle below?
Which of the following is true about the right triangle below?
Tap to reveal answer
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 45 - 90 = 45. The pictured triangle is therefore a 45-45-90 triangle. In a 45-45-90 triangle, the ratio between the two short side lengths is 1:1. Therefore, A = B. Triangles with two congruent side lengths are isosceles by definition.
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 45 - 90 = 45. The pictured triangle is therefore a 45-45-90 triangle. In a 45-45-90 triangle, the ratio between the two short side lengths is 1:1. Therefore, A = B. Triangles with two congruent side lengths are isosceles by definition.
← Didn't Know|Knew It →
When the sun is 22o above the horizon, how long is the shadow cast by a building that is 60 meters high?
When the sun is 22o above the horizon, how long is the shadow cast by a building that is 60 meters high?
Tap to reveal answer
To solve this problem, first set up a diagram that shows all of the info given in the problem.
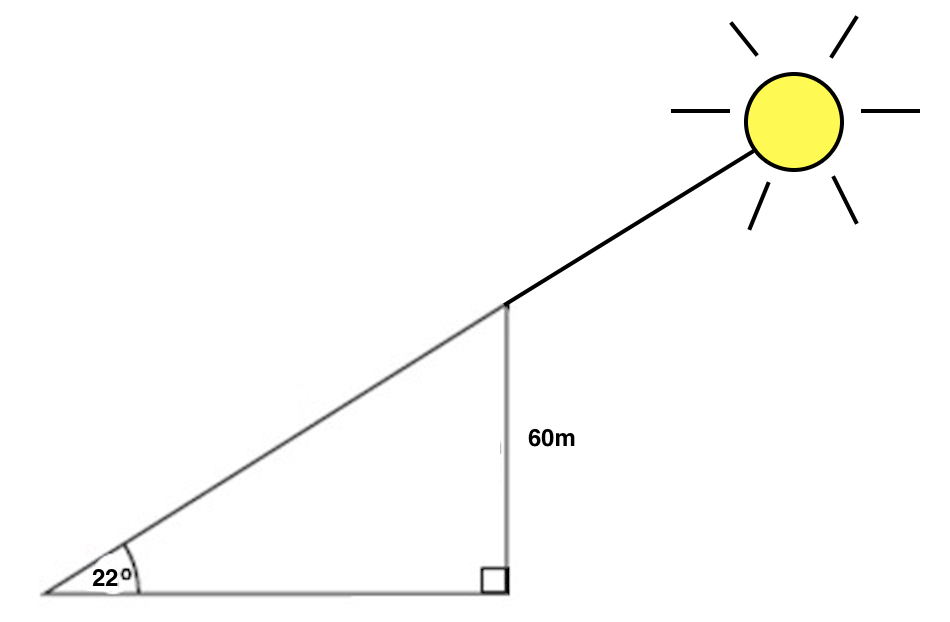
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.
Next, think about which trig functions relate our known angle, 22o, to the base (or adjacent) and the opposite sides of the triangle. If you thought tangent (or cotangent), you are correct! We know that 
and 
. For simplicity's sake, we'll use tangent to solve this problem. We have:
(Use a calculator and round to two places to find that 
)
meters
Therefore the shadow cast by the building is 150 meters long.
If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)
To solve this problem, first set up a diagram that shows all of the info given in the problem.
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we'll be solving for. We'll call this base b.
Next, think about which trig functions relate our known angle, 22o, to the base (or adjacent) and the opposite sides of the triangle. If you thought tangent (or cotangent), you are correct! We know that 
Therefore the shadow cast by the building is 150 meters long.
If you got one of the incorrect answers, you may have used sine or cosine instead of tangent, or you may have used the tangent function but inverted the fraction (adjacent over opposite instead of opposite over adjacent.)
← Didn't Know|Knew It →
Given the accompanying right triangle where 
and 
, determine the measure of 
to the nearest degree.
Given the accompanying right triangle where
Tap to reveal answer
We are given two sides of the right triangle, namely the hypotenuse and the adjacent side of the angle. Therefore, we simply use the cosine function to determine the angle:
In order to isolate the angle we must apply the inverse cosine function to both sides:
We are given two sides of the right triangle, namely the hypotenuse and the adjacent side of the angle. Therefore, we simply use the cosine function to determine the angle:
In order to isolate the angle we must apply the inverse cosine function to both sides:
← Didn't Know|Knew It →
Which of the following is not a theorem to prove that triangles are similar?
Which of the following is not a theorem to prove that triangles are similar?
Tap to reveal answer
ASA (Angle Side Angle) is a theorem to prove triangle congruency.
In this case, we only need two angles to prove that two triangles are similar, so the last side in ASA is unnecessary for this question.
For this purpose, we use the theorem AA instead.
ASA (Angle Side Angle) is a theorem to prove triangle congruency.
In this case, we only need two angles to prove that two triangles are similar, so the last side in ASA is unnecessary for this question.
For this purpose, we use the theorem AA instead.
← Didn't Know|Knew It →
Given the accompanying triangle where 
and 
, determine the length of the hypotenuse.
Given the accompanying triangle where
Tap to reveal answer
We are given the opposite side, with respect to the angle, along with the angle. Therefore, we utilize the sine function to determine the length of the hypotenuse:
Substituting the given values:
Cross multiplying:
Solving for 
:
We are given the opposite side, with respect to the angle, along with the angle. Therefore, we utilize the sine function to determine the length of the hypotenuse:
Substituting the given values:
Cross multiplying:
Solving for
← Didn't Know|Knew It →
Which of the following is true about the right triangle below?
Which of the following is true about the right triangle below?
Tap to reveal answer
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 60 - 90 = 30. The pictured triangle is therefore a 30-60-90 triangle. In a 30-60-90 triangle, the ratio between the hypotenuse and the shortest side length is 2:1. Therefore, C = 2A.
Since the pictured triangle is a right triangle, the unlabeled angle at the lower left is a right angle measuring 90 degrees. Since interior angles in a triangle sum to 180 degrees, the unlabeled angle at the upper left can be calculated by 180 - 60 - 90 = 30. The pictured triangle is therefore a 30-60-90 triangle. In a 30-60-90 triangle, the ratio between the hypotenuse and the shortest side length is 2:1. Therefore, C = 2A.
← Didn't Know|Knew It →
From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19o. How far from the boat is the top of the lighthouse?
From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is 19o. How far from the boat is the top of the lighthouse?
Tap to reveal answer
To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.
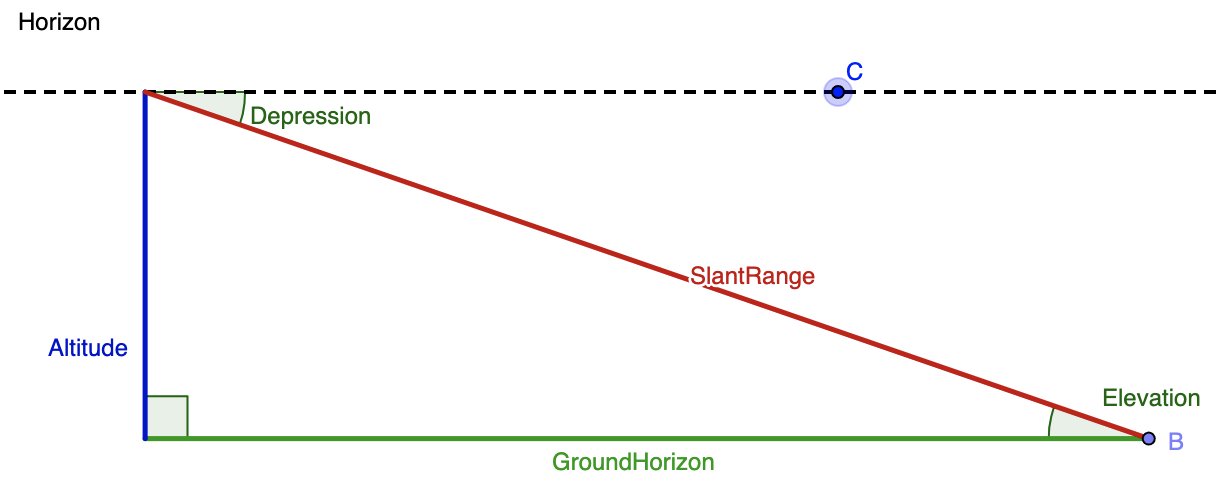
Merging together the given info and this diagram, we know that the angle of depression is 19o and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:
(where d is the distance between the top of the lighthouse and the boat)
(using a calculator in degree mode and rounding to two digits, we get that 
)
meters
To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.
Merging together the given info and this diagram, we know that the angle of depression is 19o and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we'll use that here. We get:
← Didn't Know|Knew It →
Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22o to the horizontal, how high above her starting point is she when she arrives at the lookout?
Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined 22o to the horizontal, how high above her starting point is she when she arrives at the lookout?
Tap to reveal answer
As with other trig problems, begin with a sketch of a diagram of the given and sought after information.
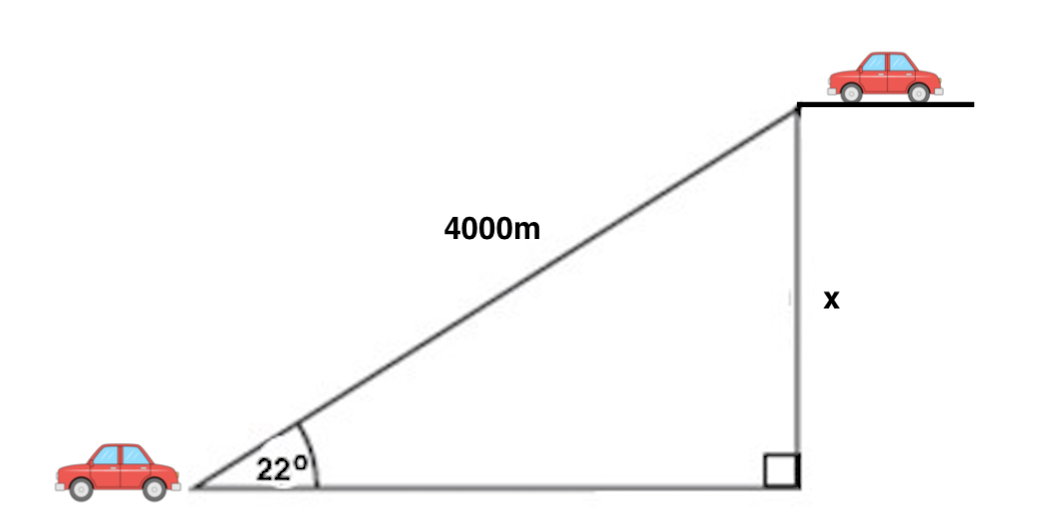
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22o. Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:
(using a calculator in degree mode and rounding to two decimals we get that 
)
Therefore the change in height between Angelina's starting and ending points is 1480 meters.
As with other trig problems, begin with a sketch of a diagram of the given and sought after information.
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is 22o. Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled x in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:
Therefore the change in height between Angelina's starting and ending points is 1480 meters.
← Didn't Know|Knew It →
Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48o. How high is the taller building?
Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is 48o. How high is the taller building?
Tap to reveal answer
To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
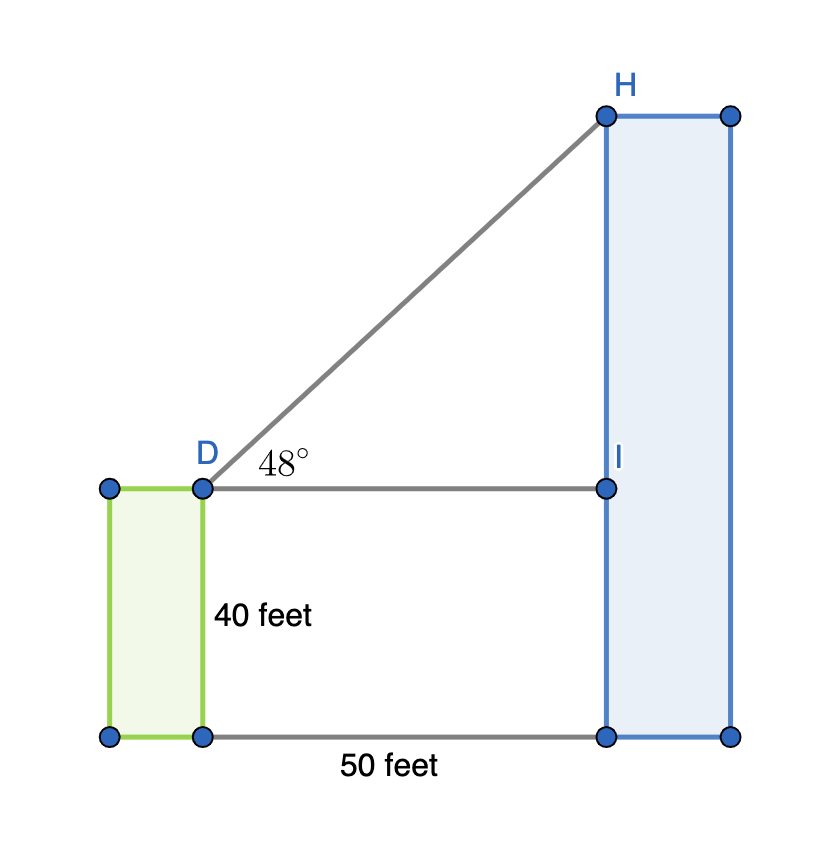
We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance 
, and then add that to the 40 foot height of the shorter building to find the entire height of the taller building. Start by finding 
:
Remember that this is not the full height of the larger building. To find that, we need to add 
feet. Therefore, the taller building is 95.5 feet tall.
To solve this problem, let's start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance 
Remember that this is not the full height of the larger building. To find that, we need to add 
← Didn't Know|Knew It →
What does the scale factor of a dilation need to be to ensure that triangles are not only similar but also congruent?
What does the scale factor of a dilation need to be to ensure that triangles are not only similar but also congruent?
Tap to reveal answer
The scale factor of a dilation tells us what we multiply corresponding sides by to get the new side lengths. In this case, we want these lengths to be the same to get congruent triangles. Thus, we must be looking for the multiplicative identity, which is 1.
The scale factor of a dilation tells us what we multiply corresponding sides by to get the new side lengths. In this case, we want these lengths to be the same to get congruent triangles. Thus, we must be looking for the multiplicative identity, which is 1.
← Didn't Know|Knew It →
All the squares are equal, and there are 6 squares in the figure.
What is the value of 
?
All the squares are equal, and there are 6 squares in the figure.
What is the value of
Tap to reveal answer
← Didn't Know|Knew It →