How to find the domain of a function

SAT Math · Learn by Concept

Help Questions

SAT Math › How to find the domain of a function

1 - 10

Which of the following functions has a domain that includes all real values of ?

$f(x)=\frac{1}{(1+x^2)}$

CORRECT

$f(x)=\frac{1}{|x-4|}$

$f(x)=\frac{1}{1+x^3}$

$f(x)=\sqrt{1-x^2}$

Explanation

The domain of a function includes all of the values of x for which that function is defined. In other words, the domain is all of the real values of x that will produce a real number. Let's look at the domains of each function one at a time.

First, let's examine $f(x)=\frac{1}{|x-4|}$

In general, when we are examining the domain of a function, we want to find places where we end up with zeros in the denominators or square-roots of negative numbers. For example, in the function $f(x)=\frac{1}{|x-4|}$ , if we let x = 4, then we would be forced to evaluate 1/0, which isn't possible. We can never divide by zero. Thus, this function is not defined over all real values of x. We can eliminate it from the answer choices.

Next, let's look at $f(x)=\frac{1}{1+x^3}$ . Let's set the denominator equal to zero to see if there are any values of x which might give us a zero in the denominator.

$1+x^3=0$

Subtract one from both sides.

$x^3 = -1$

Take the cube root of both sides.

$x=(-1)^{1/3}=-1$

Thus, if x = –1, then f(x) will be equal to 1/0, which isn't defined, because we can't divide by zero. Therefore, we can eliminate this answer choice.

Now, let's analyze $f(x)=\sqrt{1-x^2}$ .

We can never take the square root of a negative number. Thus, if $1-x^2<0$ , then f(x) won't be defined. For example, if x = 4, then $f(x)=\sqrt{-15}$ , which would produce an imaginary number. Therefore, this function can't be the correct answer.

Next, let's look at $f(x)=x^\frac{3}{2}$ . It will help us to rewrite f(x) in a form using square roots. In general, $a^{\frac{b}{c}}=\sqrt[c]{a^b}$ . As a result, we can rewrite f(x) as follows:

$f(x)=x^{\frac{3}{2}}=\sqrt{x^3}$ . In this form, we can see that if $x^3$ is negative, then f(x) won't be defined. Thus, if x = –2, for example, we would be forced to find the square root of –8, which produces an imaginary result. So, this function isn't the correct answer either.

By process of elimination the answer must be $f(x)=\frac{1}{1+x^2}$ . The reasons that this function is defined for all values of x is because the denominator can never be zero. Thus, we can pick any value of x from negative to positive infinity, and we will get a real value for f(x).

The answer is $f(x)=\frac{1}{1+x^2}$

Let .

If and are both negative integers larger than negative five, what is the smallest value possible for ?

CORRECT

Explanation

Because x and y must be negative integers greater than negative five, then x and y can only be equal to the following values:

x can equal -4, -3, -2, or -1

y can equal -4, -3, -2, or -1

Now we can try all of the combinations of x and y, and see what x # y would equal. It is helpful to note that x # y is the same as y # x because 2yx + y + x = 2xy + x + y. This means that the order of x and y doesn't matter.

-4 # -4 = 2(-4)(-4) + -4 + -4 = 24

-4 # -3 = 2(-4)(-3) + -4 + -3 = 17

-4 # -2 = 10

-4 # -1 = 3

-3 # -3 = 12

-3 # -2 = 7

-3 # -1 = 2

-2 # -2 = 4

-2 # -1 = 1

-1 # -1 = 0

We don't need to find -3 # -4, -2 # -4, etc, because x # y = y # x .

The smallest value of x # y must be 0.

What is the domain of the function f(x) = 2/(7x – 1) ?

x > (1/7)

x < (1/7)

x < (–1/7)

x > (–1/7)

x ≠ (1/7)

CORRECT

Explanation

The domain means what real number can you plug in that would still make the function work. For this case, we have to worry about the denominator so that it does not equal 0, so we solve the following. 7x – 1 = 0, 7x = 1, x = 1/7, so when x ≠ 1/7 the function will work.

Find the domain of the function:

$f(x)=\frac{x^2-1}{x-1}$

All real numbers except for 1

CORRECT

All real numbers

All real numbers except for –2

Explanation

If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into

$\left ( x+1\right )\left ( x-1\right )$

and then cancelling the 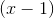$\left ( x-1\right )$ from the numerator and the denominator.

This new expression, is the equation of the function, but it will have a hole at the point where the denominator originally would have been zero. Thus, this graph will look like the line with a hole where , which is

Thus the domain of the function is all values such that $x\neq1$

What is the domain of the given function?

$f(x)=\frac{x+6}{({x+3})^2}$

x ≠ –3

CORRECT

All real numbers

x ≠ 3, –3

x ≠ 3

x ≠ 0

Explanation

The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.

Domainsqrt1

x = 0

CORRECT

x = 1

x = 1.5

x = 2

x = 3

Explanation

Domainsqrt2

Domainsqrt3

Find the domain of the following function.

$f(x)=\frac{\sqrt{x+2}}{x-3}$

$[-2,3)\cup(3,\infty)$

CORRECT

$(-2,3)\cup(3,\infty)$

$[-3,3)\cup(2,\infty)$

$\mathbb{R}$

Explanation

To find the domain, you must find all the values you can put in for x. Thus, you must figure out what values would "break" your function and give you something unable to be computed.

First we know that the number inside a square root must be positive. Thus, we can set the inside greater than or equal to 0 and solve.

$x+2\geq0 \Rightarrow x\geq-2$

We also know that the denominator of a fraction must never be 0. Thus, if we find out when it is 0, we can exclude that x value from our domain.

$x-3=0 \Rightarrow x=-3$

If we combine both of these for x, we can create an interval for our domain.

$[-2,3)\cup(3,\infty)$

Define a function $f(x) = x^{2} - 13x + 15$ .

It is desired that is domain be restricted so that has an inverse. Which of these domain restrictions would not achieve that goal?

$x \in [3,9]$

CORRECT

$x \in [-3, 3]$

$x \in [-9,- 3]$

$x \in [-15, -9]$

$x \in [9, 15 ]$

Explanation

A quadratic function has a parabola as its graph; this graph changes direction (downward to upward, or vice versa) at a given point called the vertex.

$f^{-1} (x)$ exists on a given domain interval if and only if there does not exist and on this domain such that $a \ne b$ , but . This will happen if the graph changes direction on the domain interval. The key is therefore to identify the interval that contains the vertex.

The -coordinate of the vertex of the parabola of the function

$f(x) = ax^{2}+ bx+c$

is $x = - \frac{b}{2a}$ .

The -coordinate of the vertex of the parabola of $f(x) = x^{2} - 13x + 15$ can be found by setting :

$x = - \frac{-13}{2 \cdot 1} = \frac{13}{2} = 6 \frac{1}{2}$ .

Of the five intervals in the choices,

$6 \frac{1}{2} \in [3,9]$ ,

so $f ^{-1}$ cannot exist if the domain of is restricted to this interval. This is the correct choice.

Define a function $f(x) = -2 x^{2}- 9x+ 40$ , restricting the domain to the interval .

Give the range of .

$\left [ -55, 40 \right ]$

CORRECT

$\left ( -\infty, 40 \right ]$

$\left [-55, \infty \right )$

$\left [40, 50 \frac{1}{8}\right ]$

$\left [-55 , 50 \frac{1}{8}\right ]$

Explanation

A quadratic function has a parabola as its graph; this graph changes direction at a vertex.

The -coordinate of the vertex of the parabola of the function

$f(x) = ax^{2}+ bx+c$

is $x = - \frac{b}{2a}$ .

The -coordinate of the vertex of the parabola of $f(x) = -2 x^{2}- 9x+ 40$ can be found by setting :

$x = - \frac{-9}{2 \cdot (-2)} = -\frac{9}{4} = -2 \frac{1}{4}$

$-2 \frac{1}{4} \notin [0, 5]$ , so the vertex is not on the domain. The maximum and the minimum of must occur at the endpoints, so evaluate and .

$f(0) = -2 \cdot 0 ^{2}- 9 \cdot 0 + 40$

$f(5) = -2 \cdot 5 ^{2}- 9 \cdot 5 + 40$

$= - 2 \cdot 25 - 45 +40$

The minimum and maximum values of are and 40, respectively, so the correct range is $\left [ -55, 40 \right ]$ .

Define $f(x) = \frac{1}{2}x^{2}+ 8x - 14$ , restricting the domain of the function to $\left [ 0, \infty \right )$ .

Determine $f^{-1} (x)$ (you need not determine its domain restriction).

$f^{-1}(x)= -8 + \sqrt{ 2x+ 92 }$

CORRECT

$f^{-1}(x)= -8 - \sqrt{ 2x+ 92 }$

$f^{-1}(x)= 8 - \sqrt{ 2x+ 92 }$

$f^{-1}(x)= 8 + \sqrt{ 2x+ 92 }$

$f^{-1} (x)$ does not exist

Explanation

First, we must determine whether $f^{-1} (x)$ exists.

A quadratic function has a parabola as its graph; this graph changes direction at its vertex.

$f^{-1} (x)$ exists if and only if, if , then - or, equivalently, if there does not exist and such that $a \ne b$ , but . This will happen on any interval on which the graph of constantly increases or constantly decreases, but if the graph changes direction on an interval, there will be $a \ne b$ such that on this interval. The key is therefore to determine whether the interval to which the domain is restricted contains the vertex.

The -coordinate of the vertex of the parabola of the function

$f(x) = ax^{2}+ bx+c$

is $x = - \frac{b}{2a}$ .

The -coordinate of the vertex of the parabola of $f(x) = \frac{1}{2}x^{2}+ 8x - 14$ can be found by setting $a = \frac{1}{2},b= 8$ :

$x = - \frac{8}{2\left ( \frac{1}{2} \right )} = -\frac{8}{1} = -8$ .

The vertex of the graph of without its domain restriction is at the point with -coordinate . Since $-8 \notin \left [ 0, \infty \right )$ , the vertex is not in the interior of the domain; as a consequence, $f^{-1} (x)$ exists on $\left [ 0, \infty \right )$ .

To determine the inverse of , first, rewrite in vertex form

$a = \frac{1}{2}$ , the same as in the standard form.

The graph of , if unrestricted, would have -coordinate , and -coordinate

$f(-8) = \frac{1}{2}(-8) ^{2}+ 8(-8) - 14$

$= \frac{1}{2}(64) + 8(-8) - 14$

Therefore, .

The vertex form of is therefore

$f(x)=\frac{1}{2} (x +8)^{2}- 46$

Replace with :

$y=\frac{1}{2} (x +8)^{2}- 46$

Switch and :

$x=\frac{1}{2} (y +8)^{2}- 46$

Solve for . First, add 46 to both sides:

$x+46 =\frac{1}{2} (y +8)^{2}- 46 +46$

$x+46 =\frac{1}{2} (y +8)^{2}$

Multiply both sides by 2:

$2 \cdot (x+46) =2 \cdot \frac{1}{2} (y +8)^{2}$

$2 x+92 = (y +8)^{2}$

Take the square root of both sides:

$y+8 = \pm \sqrt{ 2x+ 92 }$

Subtract 8 from both sides

$y+8 - 8 = \pm \sqrt{ 2x+ 92 } - 8$

$y = -8 \pm \sqrt{ 2x+ 92 }$

Replace with $f^{-1}(x)$ :

$f^{-1}(x)= -8 \pm \sqrt{ 2x+ 92 }$

Either $f^{-1}(x)= -8 - \sqrt{ 2x+ 92 }$ or $f^{-1}(x)= -8 + \sqrt{ 2x+ 92 }$

The domain of is the set of nonnegative numbers; this is consequently the range of $f^{-1}(x)$ . $f^{-1}(x)= -8 - \sqrt{ 2x+ 92 }$ can only have negative values, so the only possible choice for $f^{-1}(x)$ is $f^{-1}(x)= -8 + \sqrt{ 2x+ 92 }$ .

Return to subject

AI Study CoachYour personal study buddy

Instant TutoringConnect with a tutor now

Request a TutorGet matched with an expert

Live ClassesJoin interactive classes

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Practice TestsTest your skills with exam questions

QuizzesTest your knowledge with a quiz

GamesLearn through free games