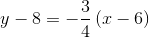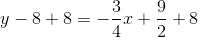SAT Subject Test in Math II - Graphing Linear Functions

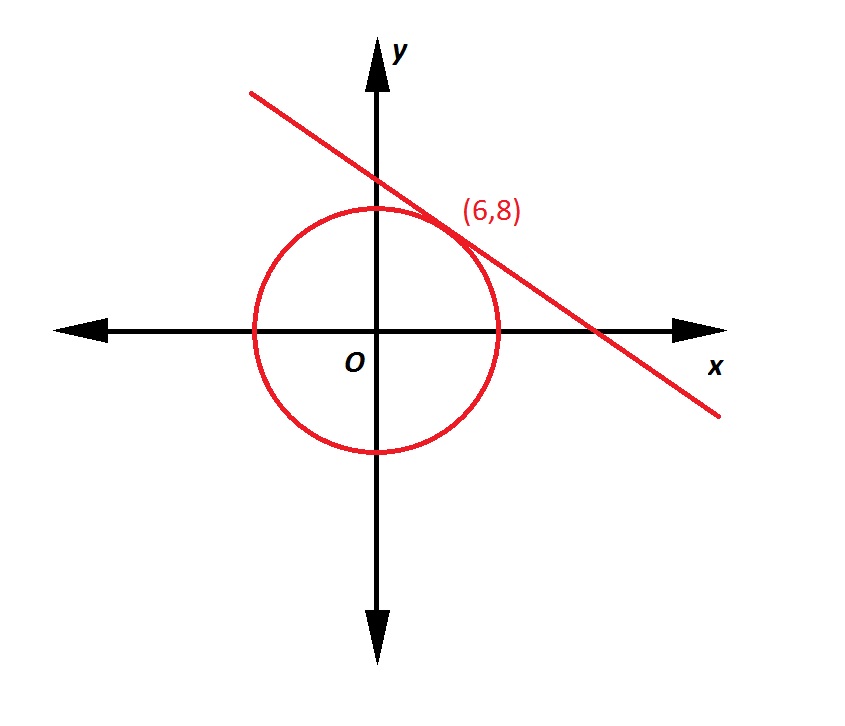
Circle

Note: Figure NOT drawn to scale.

Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?

$y = - \frac{3}{4} x+ \frac{25}{2}$

CORRECT

Insufficient information is given to determine the equation of the line.

$y = \frac{3}{4} x+ \frac{7}{2}$

$y = - \frac{4}{3} x+ 16$

$y = \frac{4}{3} x$

Explanation

A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints , has slope

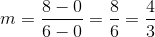
$m = \frac{8-0}{6-0} = \frac{8}{6} = \frac{4}{3}$ .

The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be $-\frac{3}{4}$ . Since it includes point , we can use the point-slope form of the line to find its equation:

$y - y_{1} = m(x-x_{1})$

$y - 8= - \frac{3}{}4\left ( x-6 \right )$

$y - 8= - \frac{3}{4} x+ \frac{9}{2}$

$y - 8+ 8 = - \frac{3}{4} x+ \frac{9}{2} + 8$

$y = - \frac{3}{4} x+ \frac{25}{2}$

Graphing Linear Functions

Help Questions

Explanation