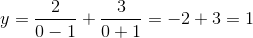X-intercept and y-intercept

SAT Subject Test in Math I · Learn by Concept

Help Questions

SAT Subject Test in Math I › X-intercept and y-intercept

1 - 10

Find the y-intercept of the following line.

CORRECT

$\small 3$

$\small -12$

Explanation

To find the y-intercept of any line, we must get the equation into the form

where m is the slope and b is the y-intercept.

To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.

To isolate y, we now must divide each side by 3.

$\frac{3y}{3}=\frac{-4x}{3}-\frac{12}{3}$

$y=\frac{-4}{3}x-4$

Now that our equation is in the desired form, our y-intercept is simply

$\small b=-4$

What are the -intercepts of the following equation?

Round each of your answers to the nearest tenth.

and

CORRECT

and

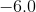
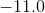
Explanation

There are two ways to solve this. First, you could substitute in for :

Take the square-root of both sides and get:

$y-5 = \pm11$

$y=5\pm11$

Therefore, your two answers are and .

You also could have done this by noticing that the problem is a circle of radius , shifted upward by .

What is the x-intercept of the given equation?

$\frac{1}{2}$

CORRECT

$-\frac{1}{3}$

$-\frac{1}{2}$

$\frac{1}{6}$

Explanation

In order to determine the x-intercept, we will need to let , and solve for .

Divide both sides by two.

$\frac{2x}{2}=\frac{1}{2}$

The answer is: $\frac{1}{2}$

What is the -intercept of the following equation?

None of the others

CORRECT

Explanation

The easiest way to solve for this kind of simple -intercept is to set equal to . You can then solve for the value in order to find the relevant intercept.

Solve for :

Divide both sides by 40:

What is the x-intercept of the above equation?

CORRECT

Explanation

To find the x-intercept, you must plug in for .

This gives you,

and you must solve for .

First, add to both sides which gives you,

Then divide both sides by to get,

Solve for the -intercepts of this equation:

$\frac{3x+4+y}{x-2} = 2x+5$

Round each of your answers to the nearest tenth.

and

CORRECT

and

Explanation

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting for . Then, we need to get it into standard form:

$\frac{3x+4+0}{x-2} = 2x+5$

Recall that the general form of the quadratic formula is:

$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

$\frac{2\pm\sqrt{(-2)^2-4(2)(-14)}}{2(2)}$

Simplifying, you get:

$\frac{2\pm\sqrt{4+112}}{4}$

$\frac{2\pm\sqrt{116}}{4}$

Using a calculator, you will get:

and

Find the -intercepts of the following equation:

Round each of your answers to the nearest tenth.

and

CORRECT

and

Explanation

Recall that the general form of the quadratic formula is:

$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

$\frac{-5\pm\sqrt{5^2-4(1)(2)}}{2(2)}$

Simplifying, you get:

$\frac{-5\pm\sqrt{25-8}}{4}$

$\frac{-5\pm\sqrt{17}}{4}$

Using a calculator, you will get:

and

What is the y-intercept of the function? $y=\frac{2}{x-1}+\frac{3}{x+1}$

CORRECT

$\textup{Does not exist.}$

$\frac{1}{5}$

Explanation

The y-intercept is the value of when .

Substitute zero into the x-variable in the equation.

$y=\frac{2}{0-1}+\frac{3}{0+1} = -2+3 = 1$

The y-intercept is .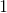

The answer is:

Find the -intercepts of the following equation:

Round each of your answers to the nearest tenth.

and

CORRECT

and

Explanation

There are two ways to solve this. First, you could substitute in for :

Take the square-root of both sides and get:

$y+14 = \pm5$

$y= -14\pm5$

Therefore, your two answers are and .

You also could have done this by noticing that the problem is a circle of radius , shifted downward by .

Solve for the -intercepts of this equation:

Round each of your answers to the nearest tenth.

and

CORRECT

and

Explanation

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting for :