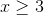Solving Inequalities

SAT Subject Test in Math I · Learn by Concept

Help Questions

SAT Subject Test in Math I › Solving Inequalities

1 - 6

Give the solution set of the inequality

$\frac{2x-5}{x-7} > 0$

$\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 7, \infty\right )$

CORRECT

$\left ( 2\frac{1}{2}, 7 \right )$

$\left (-\infty, 2\frac{1}{2} \right )$

$\left ( 2\frac{1}{2}, 7 \right )\cup \left ( 7, \infty\right )$

$\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 2\frac{1}{2}, 7 \right ) \cup \left ( 7, \infty\right )$

Explanation

Two numbers of like sign have a positive quotient.

Therefore, $\frac{2x-5}{x-7} > 0$ has as its solution set the set of points at which and are both positive or both negative.

To find this set of points, we identify the zeroes of both expressions.

$x = 2\frac{1}{2}$

Since $\frac{2x-5}{x-7}$ is nonzero we have to exclude $x = 2\frac{1}{2}$ ; is excluded anyway since it would bring about a denominator of zero. We choose one test point on each of the three intervals $\left (-\infty, 2\frac{1}{2} \right ) , \left ( 2\frac{1}{2}, 7 \right ) , \left ( 7, \infty\right )$ and determine where the inequality is correct.

$\left (-\infty, 2\frac{1}{2} \right )$

Choose :

$\frac{2 \cdot 0-5}{0-7} = \frac{-5}{-7} = \frac{5}{7} > 0$ - True.

$\left ( 2\frac{1}{2}, 7 \right )$

Choose :

$\frac{2 \cdot 3-5}{3-7} = \frac{6}{-4} =- \frac{3}{2} > 0$ - False.

$\left ( 7, \infty\right )$

Choose :

$\frac{2 \cdot 8-5}{8-7} = \frac{11}{1} =11> 0$ - True.

The solution set is $\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 7, \infty\right )$

Solve for x.

$3x+2\geq -7$

$x\geq -3$

CORRECT

$x\leq -3$

$x\geq -1$

$x\geq 1$

$x\geq 3$

Explanation

Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, subtract 2from each side.

$3x+2-2\geq -7-2$

$3x\geq -9$

Now, divide both sides by 2.

$x\geq -3$

Solve the inequality: $2x+6\leq 9x-3$

$x\geq\frac{9}{7}$

CORRECT

$x\geq-\frac{9}{7}$

$x\leq-\frac{9}{7}$

$x\leq-\frac{3}{11}$

$x\geq-\frac{3}{11}$

Explanation

Subtract on both sides.

$2x+6-2x\leq 9x-3-2x$

$6\leq 7x-3$

Add 3 on both sides.

$6+3\leq 7x-3+3$

$9\leq 7x$

Divide by 7 on both sides.

$\frac{9}{7}\leq \frac{7x}{7}$

$\frac{9}{7}\leq x$

The answer is: $x\geq\frac{9}{7}$

Solve for x.

$2x-7\geq 1$

$x\geq 4$

CORRECT

$x\geq 5$

$x\geq -3$

$x\leq 4$

Explanation

Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, add 7 to each side.

$2x-7+7\geq 1+7$