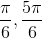Sine, Cosine, Tangent

SAT Subject Test in Math I · Learn by Concept

Help Questions

SAT Subject Test in Math I › Sine, Cosine, Tangent

1 - 9

Determine the exact value of .

$4\sqrt2$

CORRECT

$8\sqrt2$

$6\sqrt2$

$\frac{\sqrt2}{8}$

$\frac{\sqrt2}{4}$

Explanation

The exact value of is the x-value when the angle is 45 degrees on the unit circle.

The x-value of this angle is $\frac{\sqrt2}{2}$ .

$8cos(45)= 8\left(\frac{\sqrt{2}}{2}\right)=4\sqrt2$

In a triangle, , what is the measure of angle A if the side opposite of $\angleA$ angle A is 3 and the adjacent side to angle A is 4?

(Round answer to the nearest tenth of a degree.)

$36.9^{\circ}$

CORRECT

$40^{\circ}$

$32^{\circ}$

$34.7^{\circ}$

Explanation

To find the measure of angle of A we will use tangent to solve for A. We know that

$tan A=\frac{opposite}{adjacent}$

In our case opposite = 3 and adjacent = 4, we substitute these values in and get:

$tan A= \frac{3}{4}$

Now we take the inverse tangent of each side to find the degree value of A.

$A= tan^{^{-1}}\left(\frac{3}{4}\right)$

Solve for $\theta$ between $[0,2\pi]$ .

$\cos (2\theta )=\frac{1}{2}$

$\frac{\pi}{6},\frac{5\pi}{6}$

CORRECT

$\frac{\pi}{3},\frac{5\pi}{3}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{12},\frac{5\pi}{12}$

Explanation

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{3},\frac{5\pi}{3}$

Now, plug it in:

$2\theta =\frac{\pi}{3}\Rightarrow \theta =\frac{\pi}{6},$

$2\theta =\frac{5\pi}{3}\Rightarrow \theta =\frac{5\pi}{6}$

Sine

Which of the following is equal to cos(x)?

CORRECT

Explanation

Remember SOH-CAH-TOA! That means:

$\small cos(x)=\frac{adjacent}{hypotenuse}=\frac{b}{c}$

$\small \small \small sin(x)=\frac{a}{c}$ $\small \small \small \small \small sin(y)=\frac{b}{c}$

$\small \small \small \small cos(y)=\frac{a}{c}$

$\small \small \small \small \small tan(x)=\frac{a}{b}$ $\small \small \small \small tan(y)=\frac{b}{a}$

sin(y) is equal to cos(x)

If , what is if is between and $2\pi$ ?

$-\frac{\sqrt{3}}{2}$

CORRECT

$\frac{\sqrt{3}}{2}$

Explanation

Recall that $sin(\frac{\pi}{6}) =0.5$ .

Therefore, we are looking for $sin(8*\frac{\pi}{6})$ or $sin(\frac{4\pi}{3})$ .

Now, this has a reference angle of $\frac{\pi}{3}$ , but it is in the third quadrant. This means that the value will be negative. The value of $sin(\frac{\pi}{3})$ is $\frac{\sqrt{3}}{2}$ . However, given the quadrant of our angle, it will be $-\frac{\sqrt{3}}{2}$ .

Solve for $\theta$ between $[0,2\pi]$ .

$\sin (2\theta )=\frac{1}{2}$

$\frac{\pi}{12},\frac{5\pi}{12}$

CORRECT

$\frac{\pi}{6},\frac{5\pi}{6}$

$\frac{\pi}{3},\frac{2\pi}{3}$

$\frac{\pi}{6},\frac{\pi}{3}$

Explanation

First we must solve for when sin is equal to 1/2. That is at

$\frac{\pi}{6},\frac{5\pi}{6}$

Now, plug it in:

$2\theta =\frac{\pi}{6}\Rightarrow \theta =\frac{\pi}{12}$

$2\theta =\frac{5\pi}{6}\Rightarrow \theta =\frac{5\pi}{12}$

Calculate $tan(\frac{4\pi}{3})$ .

$\sqrt{3}$

CORRECT

$-\sqrt{3}$

Explanation

The tangent function has a period of $\pi$ units. That is,

$tan(x+n\pi)=tanx$

for all $n\in\mathbb{Z}$ .

Since $\frac{4\pi}{3}=\frac{\pi}{3}+\pi$ , we can rewrite the original expression $tan(\frac{4\pi}{3})$ as follows:

$tan(\frac{4\pi}{3})=tan(\frac{\pi}{3}+\pi)$

$=tan(\frac{\pi}{3})$

$=\frac{sin(\frac{\pi}{3})}{cos(\frac{\pi}{3})}$

$=\frac{(\frac{\sqrt{3}}{2})}{(\frac{1}{2})}$

$=\sqrt{3}$

Hence,

$tan(\frac{4\pi}{3})=\sqrt{3}$

Find the value of $\frac{1}{2}sin(45)+ tan(60)$ .

$\frac{\sqrt2+4\sqrt3}{4}$

CORRECT

$\frac{\sqrt2+4\sqrt3}{2}$

$\frac{3\sqrt2+\sqrt3}{12}$

$\frac{\sqrt2-4\sqrt3}{2}$

$\sqrt2+\sqrt3$

Explanation

To find the value of $\frac{1}{2}sin(45)+ tan(60)$ , solve each term separately.

$\frac{1}{2}sin(45)=\frac{1}{2} \cdot \frac{\sqrt2}{2} = \frac{\sqrt2}{4}$

$tan(60) = \sqrt3$

Sum the two terms.

$\frac{\sqrt2}{4}+\sqrt3 = \frac{\sqrt2}{4}+\frac{4\sqrt3}{4} = \frac{\sqrt2+4\sqrt3}{4}$

Calculate $cos(\frac{5\pi}{3})$ .

$\frac{1}{2}$

CORRECT

$-\frac{1}{2}$

$\frac{\sqrt{3}}{2}$

$-\frac{\sqrt{3}}{2}$

Explanation

First, convert the given angle measure from radians to degrees:

$cos(\frac{5\pi}{3})=cos(300^{\circ})$

Next, recall that $300^{\circ}$ lies in the fourth quadrant of the unit circle, wherein the cosine is positive. Furthermore, the reference angle of $300^{\circ}$ is