Range and Domain
SAT Subject Test in Math I · Learn by Concept
Help Questions
SAT Subject Test in Math I › Range and Domain
Which of the following is NOT a function?
Explanation
A function has to pass the vertical line test, which means that a vertical line can only cross the function one time. To put it another way, for any given value of 












What is the domain of the following function? Please use interval notation.
Explanation
A basic knowledge of absolute value and its functions is valuable for this problem. However, if you do not know what the typical shape of an absoluate value function looks like, one can always plug in 
Upon doing so, we learn that the 
If we plug in -100000 for 

If we plug in 100000 for 

Additionally, if we plug in any value for 

**Extra Note: Due to the absolute value notation, the negative (-) next to the 


Give the domain of the function below.
Explanation
The domain is the set of possible value for the 

Now we can solve for 
There is no real value of 
The radicand is always positive, and 


If 

Explanation
Using 



Therefore 

Domain: All real numbers
Range:
Domain: All real numbers
Range:
Explanation
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 


Find the domain:
Explanation
To find the domain, find all areas of the number line where the fraction is defined.

Factor by finding two numbers that sum to -2 and multiply to 1. These numbers are -1 and -1.
What is the domain of
Explanation
The domain refers to all the possible x-values that can be existent on the given function. Do not confuse this with the range, since this represents all the existent y-values on the graph.
Since there are no discontinuities for any x-value that we may substitute, the domain is all real numbers.
The answer is:
What is the domain of the function?
Explanation
The domain of a function refers to the viable 
Let's start with the radical, which must be greater than or equal to zero:
Next, we will look at the fraction denominator, which cannot equal zero:
Our final answer will be the union of the two sets.
Minimum: 2 (inclusive), maximum: infinity
Exclusion: 22
Domain:
What is the domain of the function?
Explanation
There are two limitations in the function: the radical and the denominator term. A radical cannot have a negative term, and a denominator cannot be equal to zero. Based on the first restriction (the radical), our 

Minimum: 0 (inclusive), maximum: infinity
Exclusion: 4
Domain:
Define the functions 

Give the natural domain of the composite function 
The set of all real numbers
Explanation
The natural domain of the composite function 
One set is the natural domain of 

The other set is the set of all values of 





Therefore, the other set is the set of all 
Substitute:
This holds for all real numbers, so this set is also the set of all real numbers.
The natural domain of 





















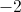



 is a sine curve. What are the domain and range of this function?
is a sine curve. What are the domain and range of this function?















![(-\infty,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/922624/gif.latex)














![[0,4]\cup [4,\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/211092/gif.latex)













