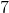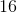Exponents and Logarithms

When adding exponents, we don't add the exponents or multiply out the bases. Our goal is to see if we can factor anything. We do see three . Let's factor.

Remember when multiplying exponents, we just add the powers.

Using the Product of Powers Rule, then the Power of a Power Rule, rewrite the first term:

Substitute for ; the equation becomes

,

which is quadratic in terms of . The trinomial might be factorable using the method, where we split the middle term with integers whose product is and whose sum is 11. By trial and error, we find the integers to be 12 and , so the equation can be written as follows:

Factoring by grouping:

By the Zero Product Rule, one of these two factors must be equal to 0.

If , then .

Substituting back for , we get

.

This is impossible, since any power of a positive number must be positive.

If , then:

Substituting back for , we get

Since ,

it holds that , and , the only solution.

By the Power of a Power and Product of Power Rules, we can rewrite this equation as

Substitute for ; the resulting equation is the quadratic equation

,

which can be written in standard form by subtracting from both sides:

The quadratic trinomial fits the perfect square trinomial pattern:

By the square root principle,

Substituting for :

When dealing with subtraction in regards to logarithms, it's the same as dividing the numbers.

, so the equation

can be rewritten as:

By the Power of a Power rule:

It follows that

Solving for :

A set with elements has subsets.

Solve:

When dealing with addition in regards to logarithms, it's the same as multiplying the numbers.

is the same as . Let's factor out . It's the same as . Therefore which is the answer to our question.

Using the properties of logarithms

and ,

we simplify as follows:

Take the natural logarithm of both sides:

By Logarithm of a Power Rule, the above becomes

After distributing, solve for :

Factor out the left side, then divide:

Substituting the values of the logarithms:

This rounds to 0.45.