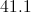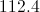Applying the Law of Cosines

Math · Learn by Concept

Help Questions

Math › Applying the Law of Cosines

1 - 3

1

In $\Delta ABC$ , , , and . To the nearest tenth, what is $m \angle A$ ?

$81.3 ^{\circ }$

CORRECT

A triangle with these sidelengths cannot exist.

0

$81.3 ^{\circ }\textrm{ or } 98.7^{ \circ }$

0

$98.7^{ \circ }$

0

$171.3^{ \circ }$

0

Explanation

By the Triangle Inequality, this triangle can exist, since .

By the Law of Cosines:

$\left ( BC\right )^{2} = \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A$

Substitute the sidelengths and solve for $\cos m \angle A$ :

$32^{2} = 26^{2} + 23^{2} - 2\cdot 26 \cdot 23 \cdot \cos m \angle A$

$1,024 =676 + 529 - 1,196 \cdot \cos m \angle A$

$1,024 =1,205 - 1,196 \cdot \cos m \angle A$

$-181 = - 1,196 \cdot \cos m \angle A$

$\cos m \angle A = 181 \div 1,196 \approx 0.1513$

$m \angle A \approx \cos^{-1} 0.1513 \approx 81.3 ^{\circ }$

2

A triangle has sides of length 12, 17, and 22. Of the measures of the three interior angles, which is the greatest of the three?

$97.2^{\circ }$

CORRECT

$130.1^{\circ }$

0

$93.6^{\circ }$

0

$119.2^{\circ }$

0

$86.4^{\circ }$

0

Explanation

We can apply the Law of Cosines to find the measure of this angle, which we will call :

$c^{2} = a^{2} + b^{2} -2ab \cos C$

The widest angle will be opposite the side of length 22, so we will set:

, ,

$22^{2} = 12^{2} + 17^{2} -2\cdot 12\cdot 17 \cos C$

$484 = 144 + 289 -408 \cos C$

$51= -408 \cos C$

$\cos C = -\frac{51}{408} = -0.125$

$C = \cos^{-1} 0.125 = 97.2^{\circ }$

3

In $\Delta ABC$ , $m \angle A = 66^{\circ }$ , , and . To the nearest tenth, what is ?

CORRECT

0

0

0

A triangle with these characteristics cannot exist.

0

Explanation

By the Law of Cosines:

$\left ( BC\right )^{2} = \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A$

or, equivalently,

$BC =\sqrt{ \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A}$

Substitute:

$BC =\sqrt{ 26^{2} +23^{2} - 2 \cdot 26 \cdot 23 \cdot \cos 66 ^{\circ }}$

$\approx \sqrt{ 676 +529 - 1,196 \cdot 0.4067}$

$\approx \sqrt{ 718.6} \approx 26.8$

Return to subject

AI Study CoachYour personal study buddy

Instant TutoringConnect with a tutor now

Request a TutorGet matched with an expert

Live ClassesJoin interactive classes

Questions of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games