Solid Geometry - Math
Card 1 of 640
The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?
The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?
Tap to reveal answer
Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height
LA = 2B
π(r)(l) = 2π(r2)
rl = 2r2
l = 2r

From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields
r2 + 92 = (2r)2
r2 + 81 = 4r2
81 = 3r2
27 = r2
B = π(r2) = 27π
LA = 2B = 2(27π) = 54π
SA = B + LA = 81π
Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height
LA = 2B
π(r)(l) = 2π(r2)
rl = 2r2
l = 2r

From the diagram, we can see that r2 + h2 = l2. Since h = 9 and l = 2r, some substitution yields
r2 + 92 = (2r)2
r2 + 81 = 4r2
81 = 3r2
27 = r2
B = π(r2) = 27π
LA = 2B = 2(27π) = 54π
SA = B + LA = 81π
← Didn't Know|Knew It →
What is the surface area of a cone with a radius of 6 in and a height of 8 in?
What is the surface area of a cone with a radius of 6 in and a height of 8 in?
Tap to reveal answer
Find the slant height of the cone using the Pythagorean theorem: _r_2 + _h_2 = _s_2 resulting in 62 + 82 = _s_2 leading to _s_2 = 100 or s = 10 in
SA = πrs + πr_2 = π(6)(10) + π(6)2 = 60_π + 36_π_ = 96_π_ in2
60_π_ in2 is the area of the cone without the base.
36_π_ in2 is the area of the base only.
Find the slant height of the cone using the Pythagorean theorem: _r_2 + _h_2 = _s_2 resulting in 62 + 82 = _s_2 leading to _s_2 = 100 or s = 10 in
SA = πrs + πr_2 = π(6)(10) + π(6)2 = 60_π + 36_π_ = 96_π_ in2
60_π_ in2 is the area of the cone without the base.
36_π_ in2 is the area of the base only.
← Didn't Know|Knew It →
What is the surface area of a cone with a radius of 4 and a height of 3?
What is the surface area of a cone with a radius of 4 and a height of 3?
Tap to reveal answer
Here we simply need to remember the formula for the surface area of a cone and plug in our values for the radius and height.

Here we simply need to remember the formula for the surface area of a cone and plug in our values for the radius and height.
← Didn't Know|Knew It →
What is the surface area of a cone with a height of 8 and a base with a radius of 5?
What is the surface area of a cone with a height of 8 and a base with a radius of 5?
Tap to reveal answer
To find the surface area of a cone we must plug in the appropriate numbers into the equation

where  is the radius of the base, and
is the radius of the base, and  is the lateral, or slant height of the cone.
is the lateral, or slant height of the cone.
First we must find the area of the circle.
To find the area of the circle we plug in our radius into the equation of a circle which is 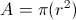
This yields  .
.
We then need to know the surface area of the cone shape.
To find this we must use our height and our radius to make a right triangle in order to find the lateral height using Pythagorean’s Theorem.
Pythagorean’s Theorem states 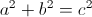
Take the radius and height and plug them into the equation as a and b to yield 
First square the numbers 
After squaring the numbers add them together 
Once you have the sum, square root both sides 
After calculating we find our length is 
Then plug the length into the second portion of our surface area equation above to get 
Then add the area of the circle with the conical area to find the surface area of the entire figure 
The answer is  .
.
To find the surface area of a cone we must plug in the appropriate numbers into the equation
where 

First we must find the area of the circle.
To find the area of the circle we plug in our radius into the equation of a circle which is
This yields 
We then need to know the surface area of the cone shape.
To find this we must use our height and our radius to make a right triangle in order to find the lateral height using Pythagorean’s Theorem.
Pythagorean’s Theorem states
Take the radius and height and plug them into the equation as a and b to yield
First square the numbers
After squaring the numbers add them together
Once you have the sum, square root both sides
After calculating we find our length is
Then plug the length into the second portion of our surface area equation above to get
Then add the area of the circle with the conical area to find the surface area of the entire figure
The answer is 
← Didn't Know|Knew It →
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
You have an empty cylinder with a base diameter of 6 and a height of 10 and you have a cone full of water with a base radius of 3 and a height of 10. If you empty the cone of water into the cylinder, how much volume is left empty in the cylinder?
Tap to reveal answer
Cylinder Volume = 
Cone Volume = 
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume




Cylinder Volume =
Cone Volume =
Cylinder Diameter = 6, therefore Cylinder Radius = 3
Cone Radius = 3
Empty Volume = Cylinder Volume – Cone Volume
← Didn't Know|Knew It →
Find the surface area of a cone that has a radius of 12 and a slant height of 15.
Find the surface area of a cone that has a radius of 12 and a slant height of 15.
Tap to reveal answer
The standard equation to find the surface area of a cone is

where  denotes the slant height of the cone, and
denotes the slant height of the cone, and  denotes the radius.
denotes the radius.
Plug in the given values for  and
and  to find the answer:
to find the answer:

The standard equation to find the surface area of a cone is
where 

Plug in the given values for 

← Didn't Know|Knew It →
Find the surface area of the following cone.

Find the surface area of the following cone.

Tap to reveal answer
The formula for the surface area of a cone is:


where  is the radius of the cone and
is the radius of the cone and  is the slant height of the cone.
is the slant height of the cone.
Plugging in our values, we get:


The formula for the surface area of a cone is:
where 

Plugging in our values, we get:
← Didn't Know|Knew It →
Find the surface area of the following cone.

Find the surface area of the following cone.

Tap to reveal answer
The formula for the surface area of a cone is:



Use the Pythagorean Theorem to find the length of the radius:



Plugging in our values, we get:


The formula for the surface area of a cone is:
Use the Pythagorean Theorem to find the length of the radius:
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the surface area of the following half cone.

Find the surface area of the following half cone.

Tap to reveal answer
The formula for the surface area of the half cone is:


Where  is the radius,
is the radius,  is the slant height, and
is the slant height, and  is the height of the cone.
is the height of the cone.
Use the Pythagorean Theorem to find the height of the cone:



Plugging in our values, we get:



The formula for the surface area of the half cone is:
Where 


Use the Pythagorean Theorem to find the height of the cone:
Plugging in our values, we get:
← Didn't Know|Knew It →
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
What is the volume of a right cone with a diameter of 6 cm and a height of 5 cm?
Tap to reveal answer
The general formula is given by  , where
, where  = radius and
= radius and  = height.
= height.
The diameter is 6 cm, so the radius is 3 cm.

The general formula is given by 


The diameter is 6 cm, so the radius is 3 cm.
← Didn't Know|Knew It →
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
There is a large cone with a radius of 4 meters and height of 18 meters. You can fill the cone with water at a rate of 3 cubic meters every 25 seconds. How long will it take you to fill the cone?
Tap to reveal answer
First we will calculate the volume of the cone

Next we will determine the time it will take to fill that volume

We will then convert that into minutes

First we will calculate the volume of the cone
Next we will determine the time it will take to fill that volume
We will then convert that into minutes
← Didn't Know|Knew It →
What is the volume of a cone with a height of  and a base with a radius of
and a base with a radius of  ?
?
What is the volume of a cone with a height of 

Tap to reveal answer
To find the volume of a cone we must use the equation  . In this formula,
. In this formula,  is the area of the circular base of the cone, and
is the area of the circular base of the cone, and  is the height of the cone.
is the height of the cone.
We must first solve for the area of the base using  .
.
The equation for the area of a circle is  . Using this, we can adjust our formula and plug in the value of our radius.
. Using this, we can adjust our formula and plug in the value of our radius.



Now we can plug in our given height,  .
.

Multiply everything out to solve for the volume.

The volume of the cone is  .
.
To find the volume of a cone we must use the equation 


We must first solve for the area of the base using 
The equation for the area of a circle is 
Now we can plug in our given height, 
Multiply everything out to solve for the volume.
The volume of the cone is 
← Didn't Know|Knew It →
What is the equation of a circle with a center of (5,15) and a radius of 7?
What is the equation of a circle with a center of (5,15) and a radius of 7?
Tap to reveal answer
To find the equation of a circle we must first know the standard form of the equation of a circle which is 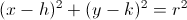
The letters  and
and  represent the
represent the  -value and
-value and  -value of the center of the circle respectively.
-value of the center of the circle respectively.
In this case  is 5 and k is 15 so plugging the values into the equation yields
is 5 and k is 15 so plugging the values into the equation yields 
We then plug the radius into the equation to get 
Square it to yield 
The equation with a center of (5,15) and a radius of 7 is  .
.
To find the equation of a circle we must first know the standard form of the equation of a circle which is
The letters 



In this case 
We then plug the radius into the equation to get
Square it to yield
The equation with a center of (5,15) and a radius of 7 is 
← Didn't Know|Knew It →
What is the volume of a cone with base radius 4, and height 6?
What is the volume of a cone with base radius 4, and height 6?
Tap to reveal answer
The volume of a cone is  , where
, where  is the height of the cone and
is the height of the cone and  is the base radius.
is the base radius.
The volume of this cone is thus:

= 
The volume of a cone is 


The volume of this cone is thus:
=
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
What is the volume of a cone that has a radius of 3 and a height of 4?
What is the volume of a cone that has a radius of 3 and a height of 4?
Tap to reveal answer
The standard equation for the volume of a cone is

where  denotes the radius and
denotes the radius and  denotes the height.
denotes the height.
Plug in the given values for  and
and  to find the answer:
to find the answer:

The standard equation for the volume of a cone is
where 

Plug in the given values for 

← Didn't Know|Knew It →
Find the volume of the following cone.

Find the volume of the following cone.

Tap to reveal answer
The formula for the volume of a cone is:

where  is the radius of the cone and
is the radius of the cone and  is the height of the cone.
is the height of the cone.
In order to find the height of the cone, use the Pythagorean Theorem:




Plugging in our values, we get:


The formula for the volume of a cone is:
where 

In order to find the height of the cone, use the Pythagorean Theorem:
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the volume of the following cone.

Find the volume of the following cone.

Tap to reveal answer
The formula for the volume of a cone is:

Where  is the radius of the cone and
is the radius of the cone and  is the height of the cone
is the height of the cone
Use the Pythagorean Theorem to find the length of the radius:



Plugging in our values, we get:


The formula for the volume of a cone is:
Where 

Use the Pythagorean Theorem to find the length of the radius:
Plugging in our values, we get:
← Didn't Know|Knew It →
Find the volume of the following half cone.

Find the volume of the following half cone.

Tap to reveal answer
The formula of the volume of a half cone is:


Where  is the radius of the cone and
is the radius of the cone and  is the height of the cone.
is the height of the cone.
Use the Pythagorean Theorem to find the height of the cone:





The formula of the volume of a half cone is:
Where 

Use the Pythagorean Theorem to find the height of the cone:
← Didn't Know|Knew It →
What is the surface area of an equilateral triangluar prism with edges of 6 in and a height of 12 in?
Let  and
and  .
.
What is the surface area of an equilateral triangluar prism with edges of 6 in and a height of 12 in?
Let 

Tap to reveal answer
The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.
The area of the sides is given by:  , so for all three sides we get
, so for all three sides we get  .
.
The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees. We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90. The height is the side opposite the 60 degree angle, so it becomes  or 5.196.
or 5.196.
The area for a triangle is given by  and since we need two of them we get
and since we need two of them we get  .
.
Therefore the total surface area is  .
.
The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.
The area of the sides is given by: 

The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees. We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90. The height is the side opposite the 60 degree angle, so it becomes 
The area for a triangle is given by 

Therefore the total surface area is 
← Didn't Know|Knew It →



