Geometry - Math
Card 1 of 2792
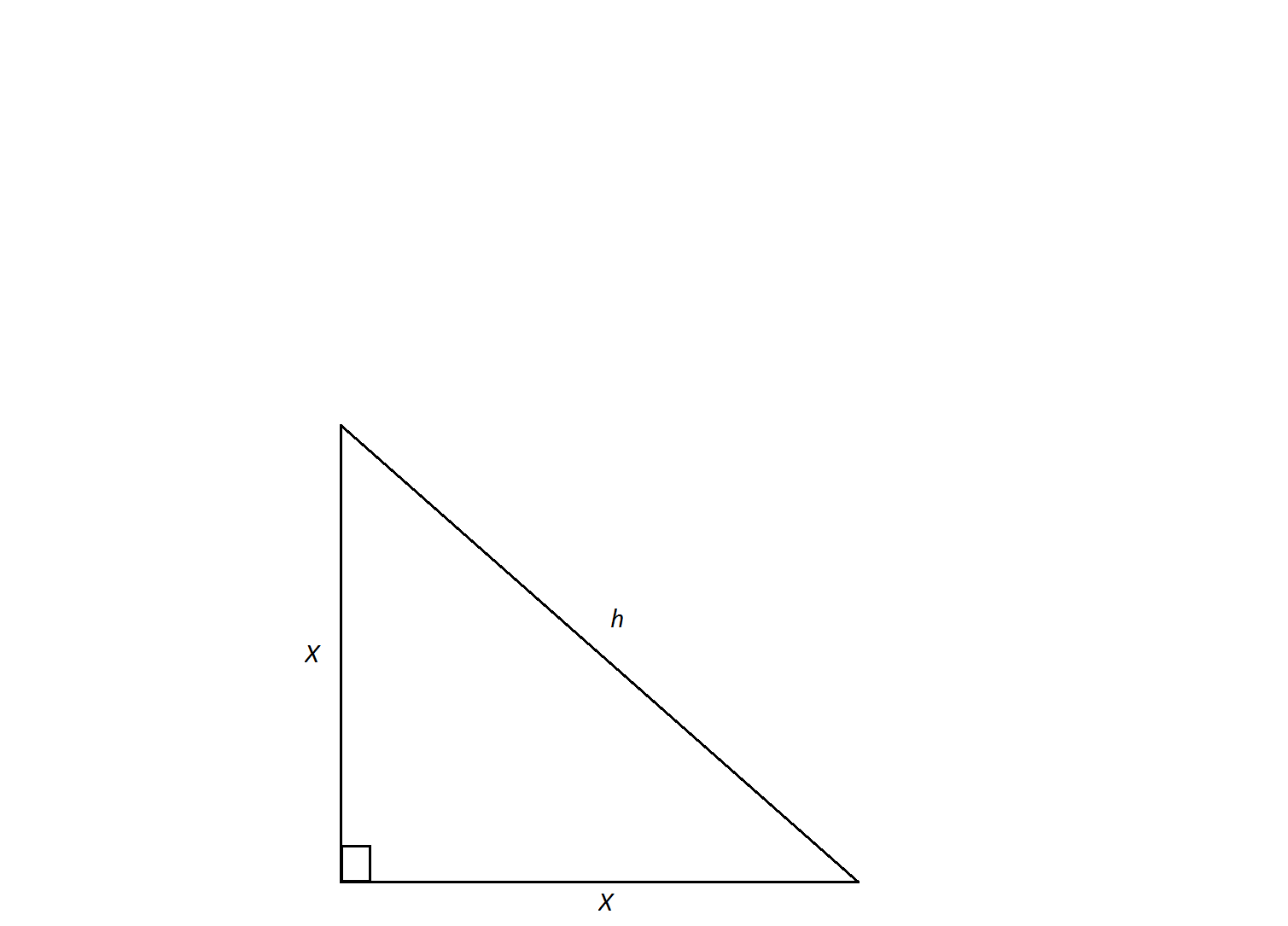
An isosceles triangle has a hypotenuse of 
. Find the length of its sides, 
.
An isosceles triangle has a hypotenuse of
Tap to reveal answer
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lengths follow a specific pattern that states you can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
← Didn't Know|Knew It →
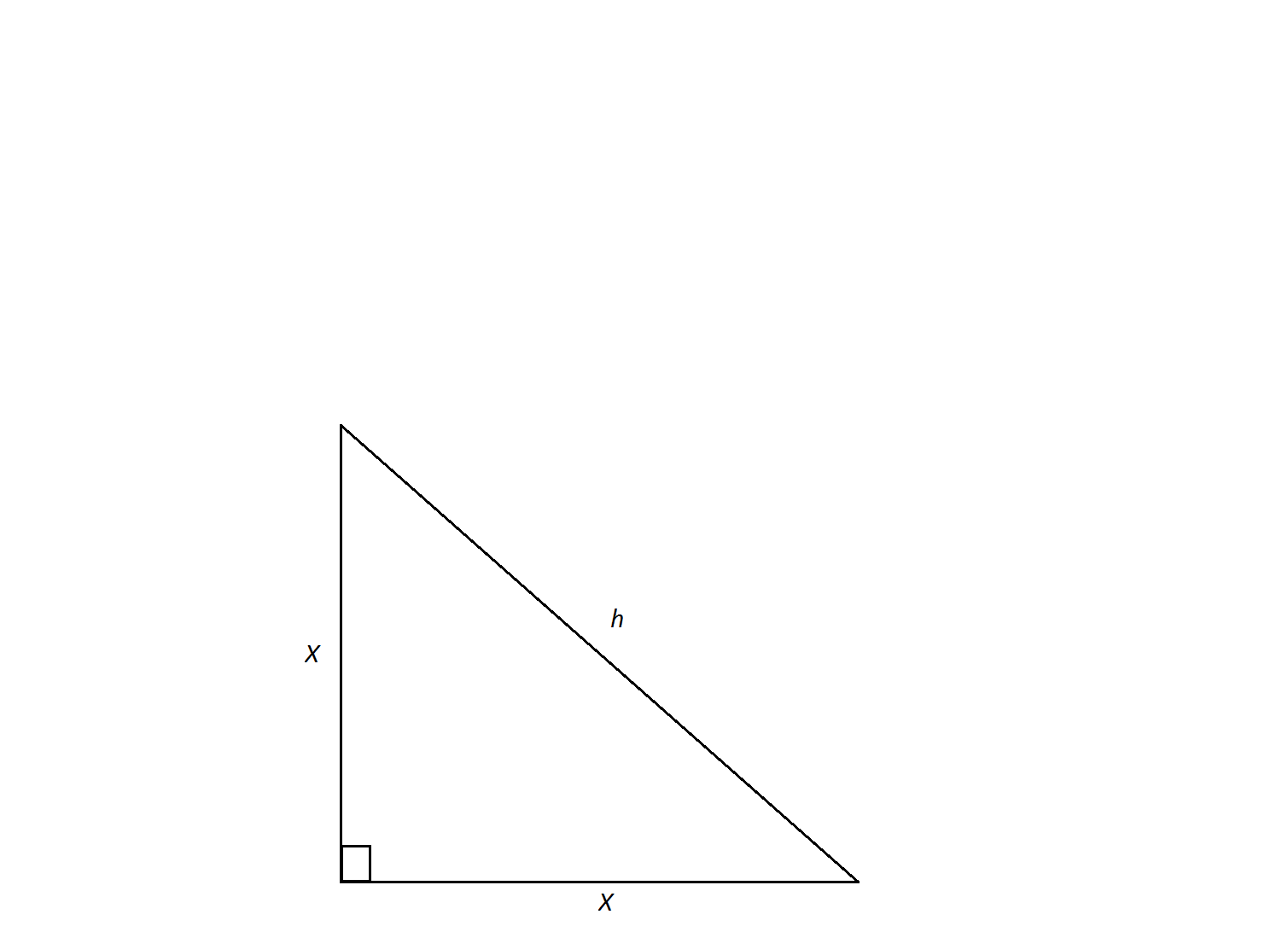
The measure of the sides of this isosceles right triangle are 
. Find the measure of its hypotenuse,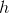 
.
The measure of the sides of this isosceles right triangle are
Tap to reveal answer
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.
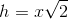
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
← Didn't Know|Knew It →
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
Tap to reveal answer
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
← Didn't Know|Knew It →
The hypotenuse of an isosceles right triangle has a measure of 
. Find its perimeter.
The hypotenuse of an isosceles right triangle has a measure of
Tap to reveal answer
In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
Now we can calculate the perimeter by doubling 
and adding 
.
In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Now we can calculate the perimeter by doubling
← Didn't Know|Knew It →
The side lengths of an isoceles right triangle measure 
. Find its perimeter.
The side lengths of an isoceles right triangle measure
Tap to reveal answer
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.
Now we can calculate the perimeter by doubling 
and adding 
.
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Now we can calculate the perimeter by doubling
← Didn't Know|Knew It →
A triangle has two angles equal to 
and two sides equal to 
. What is the perimeter of this triangle?
A triangle has two angles equal to
Tap to reveal answer
When a triangle has two angles equal to 
, it must be a 
isosceles right triangle.
The pattern for the sides of a 
is 
.
Since two sides are equal to 
, this triangle will have sides of 
.
Add them all together to get 
.
When a triangle has two angles equal to
The pattern for the sides of a
Since two sides are equal to
Add them all together to get
← Didn't Know|Knew It →
In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?
A (Angle A = 41°)
B C
In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?
A (Angle A = 41°)
B C
Tap to reveal answer
If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:
41° + 41° = 82°
Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:
180° - 82° = 98°
If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:
41° + 41° = 82°
Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:
180° - 82° = 98°
← Didn't Know|Knew It →
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
If the average of the measures of two angles in a triangle is 75o, what is the measure of the third angle in this triangle?
Tap to reveal answer
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
The sum of the angles in a triangle is 180o: a + b + c = 180
In this case, the average of a and b is 75:
(a + b)/2 = 75, then multiply both sides by 2
(a + b) = 150, then substitute into first equation
150 + c = 180
c = 30
← Didn't Know|Knew It →
Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.
Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.
Tap to reveal answer
To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
← Didn't Know|Knew It →
Which of the following can NOT be the angles of a triangle?
Which of the following can NOT be the angles of a triangle?
Tap to reveal answer
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.
← Didn't Know|Knew It →
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
Let the measures, in degrees, of the three angles of a triangle be x, y, and z. If y = 2z, and z = 0.5x - 30, then what is the measure, in degrees, of the largest angle in the triangle?
Tap to reveal answer
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:
x + y + z = 180
y = 2z
z = 0.5x - 30
If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.
Because we are told already that y = 2z, we alreay have the value of y in terms of z.
We must solve the equation z = 0.5x - 30 for x in terms of z.
Add thirty to both sides.
z + 30 = 0.5x
Mutliply both sides by 2
2(z + 30) = 2z + 60 = x
x = 2z + 60
Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.
(2z + 60) + 2z + z = 180
5z + 60 = 180
5z = 120
z = 24
Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.
Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.
The answer is 108.
← Didn't Know|Knew It →
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
Angles x, y, and z make up the interior angles of a scalene triangle. Angle x is three times the size of y and 1/2 the size of z. How big is angle y.
Tap to reveal answer
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
The answer is 18
We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:
x + y + z = 180
x = 3y
2x = z
We can solve for y and z in the second and third equations and then plug into the first to solve.
x + (1/3)x + 2x = 180
3\[x + (1/3)x + 2x = 180\]
3x + x + 6x = 540
10x = 540
x = 54
y = 18
z = 108
← Didn't Know|Knew It →
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
, which of the following is the measure of one of the angles of the triangle?
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is
Tap to reveal answer
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
← Didn't Know|Knew It →
Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is 
. The measure of angle CBD is 
. The length of segment 
is 4.
Find the measure of 
.
Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is
Find the measure of
Tap to reveal answer
The measure of 
is 
. Since 
, 
, and 
are collinear, and the measure of 
is 
, we know that the measure of 
is 
.
Because the measures of the three angles in a triangle must add up to 
, and two of the angles in triangle 
are 
and 
, the third angle, 
, is 
.
The measure of
Because the measures of the three angles in a triangle must add up to
← Didn't Know|Knew It →
Triangle ABC has angle measures as follows:
What is 
?
Triangle ABC has angle measures as follows:
What is
Tap to reveal answer
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation 
After combining like terms and cancelling, we have 
Thus 
The sum of the measures of the angles of a triangle is 180.
Thus we set up the equation
After combining like terms and cancelling, we have
Thus
← Didn't Know|Knew It →
The base angle of an isosceles triangle is 
. What is the vertex angle?
The base angle of an isosceles triangle is
Tap to reveal answer
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
for x to find the measure of the vertex angle.
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is
← Didn't Know|Knew It →
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?
Tap to reveal answer
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
= the vertex angle and 
= the base angle
So the equation to solve becomes 
Thus the vertex angle is 34 and the base angles are 73.
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let
So the equation to solve becomes
Thus the vertex angle is 34 and the base angles are 73.
← Didn't Know|Knew It →
Two interior angles in an obtuse triangle measure 
and 
. What is the measurement of the third angle.
Two interior angles in an obtuse triangle measure
Tap to reveal answer
Interior angles of a triangle always add up to 180 degrees.
Interior angles of a triangle always add up to 180 degrees.
← Didn't Know|Knew It →
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Tap to reveal answer
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
= vertex angle and 
= base angle
So the equation to solve becomes 
.
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let
So the equation to solve becomes
← Didn't Know|Knew It →
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?
Tap to reveal answer
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
= vertex angle and 
= base angle
So the equation to solve becomes 
So the vertex angle is 40 and the base angles is 70
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let
So the equation to solve becomes
So the vertex angle is 40 and the base angles is 70
← Didn't Know|Knew It →