Algebra II - Math
Card 1 of 1752
Find the distance between  and
and  on a number line.
on a number line.
Find the distance between 

Tap to reveal answer
To find the distance on a number line:




To find the distance on a number line:
← Didn't Know|Knew It →
If a card is drawn randomly from a regular shuffled 52 card deck, what is the probability that the card is either a spade or a 3?
If a card is drawn randomly from a regular shuffled 52 card deck, what is the probability that the card is either a spade or a 3?
Tap to reveal answer
How many cards in the deck are either a spade or a 3?
There are thirteen spades, including a 3 of spades.
There are four 3's, including a 3 of spades.
Since we are counting the same card (3 of spades) twice, there are actually

 distinct cards that fit the criteria of being either a spade or a 3.
distinct cards that fit the criteria of being either a spade or a 3.
Since any of the 52 cards is equally likely to be drawn, the probability that it is a spade or a 3, is
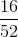

How many cards in the deck are either a spade or a 3?
There are thirteen spades, including a 3 of spades.
There are four 3's, including a 3 of spades.
Since we are counting the same card (3 of spades) twice, there are actually

Since any of the 52 cards is equally likely to be drawn, the probability that it is a spade or a 3, is
← Didn't Know|Knew It →
Without using a calculator, which of the following is the best estimate for  ?
?
Without using a calculator, which of the following is the best estimate for 
Tap to reveal answer
We know that  and
and  .
.



Because 90 falls is approximately halfway between 81 and 100, the square root of 90 is approximately halfway between 9 and 10, or 9.5.
We know that 

Because 90 falls is approximately halfway between 81 and 100, the square root of 90 is approximately halfway between 9 and 10, or 9.5.
← Didn't Know|Knew It →
Which of the following are considered real numbers?
Which of the following are considered real numbers?
Tap to reveal answer
Real numbers can be found anywhere on a continuous number line ranging from negative infinity to positive infinity; therefore, all of the numbers are real numbers.
Real numbers can be found anywhere on a continuous number line ranging from negative infinity to positive infinity; therefore, all of the numbers are real numbers.
← Didn't Know|Knew It →
Place in order from smallest to largest:

Place in order from smallest to largest:
Tap to reveal answer
To place in order, first we must find a common denominator and convert all fractions to that denominator.
 have a common denominator of
have a common denominator of  .
.
 have a common denominator of
have a common denominator of  .
.
 have a common denominator of
have a common denominator of  .
.
Therefore we can use common denominators to make all of the fractions look similar. Then the ordering becomes trivial.



To place in order, first we must find a common denominator and convert all fractions to that denominator.






Therefore we can use common denominators to make all of the fractions look similar. Then the ordering becomes trivial.
← Didn't Know|Knew It →
What number is  of
of  ?
?
What number is 

Tap to reveal answer
For percent problems there are verbal cues:
"IS" means equals and "OF" means multiplication.
Then the equation to solve becomes:

For percent problems there are verbal cues:
"IS" means equals and "OF" means multiplication.
Then the equation to solve becomes:
← Didn't Know|Knew It →
Which of the following is NOT a real number?
Which of the following is NOT a real number?
Tap to reveal answer
We are looking for a number that is not real.
 ,
,  , and
, and  are irrational numbers, but they are still real.
are irrational numbers, but they are still real.
Then,  is equivalent to
is equivalent to  by the rules of complex numbers. Thus, it is also real.
by the rules of complex numbers. Thus, it is also real.
That leaves us with:  which in fact is imaginary (since no real number multiplied by itself yields a negative number) and simplifies to
which in fact is imaginary (since no real number multiplied by itself yields a negative number) and simplifies to  .
.
We are looking for a number that is not real.



Then, 

That leaves us with: 

← Didn't Know|Knew It →
Simplify 
Simplify
Tap to reveal answer
Find the least common denominator (LCD) and convert each fraction to the LCD and then add. Simplify as necessary.

The result is an improper fraction because the numerator is larger than the denominator and can be simplified and converted to a mix numeral.

Find the least common denominator (LCD) and convert each fraction to the LCD and then add. Simplify as necessary.
The result is an improper fraction because the numerator is larger than the denominator and can be simplified and converted to a mix numeral.
← Didn't Know|Knew It →
All of the following matrix products are defined EXCEPT:
All of the following matrix products are defined EXCEPT:
Tap to reveal answer
Every matrix has a dimension, which is represented as the number of rows and columns. For example, a matrix with three rows and two columns is said to have dimension 3 x 2.
The matrix

has two rows and three columns, so its dimension is 2 x 3. (Remember that rows go from left to right, while columns run up and down.)
Matrix multiplication is defined only if the number of columns in the first matrix is equal to the number of rows on the second matrix. The easiest way to determine this is to write the dimension of each matrix. For example, let's say that one matrix has dimension a x b, and the second matrix has dimension c x d. We can only multiply the first matrix by the second matrix if the values of b and c are equal. It doesn't matter what the values of a and d are, as long as b (the number of columns in the first matrix) matches c (the number of rows in the second matrix).
Let's go back to the problem and analyze the choice  .
.
The dimension of the first matrix is 2 x 3, because it has two rows and three columns. The second matrix has dimension 2 x 2, because it has two rows and two columns.
We can't multiply these matrices because the number of columns in the first matrix (3) is not equal to the number of rows in the second matrix (2). Thus, this product is not defined.
The answer is  .
.
Every matrix has a dimension, which is represented as the number of rows and columns. For example, a matrix with three rows and two columns is said to have dimension 3 x 2.
The matrix
has two rows and three columns, so its dimension is 2 x 3. (Remember that rows go from left to right, while columns run up and down.)
Matrix multiplication is defined only if the number of columns in the first matrix is equal to the number of rows on the second matrix. The easiest way to determine this is to write the dimension of each matrix. For example, let's say that one matrix has dimension a x b, and the second matrix has dimension c x d. We can only multiply the first matrix by the second matrix if the values of b and c are equal. It doesn't matter what the values of a and d are, as long as b (the number of columns in the first matrix) matches c (the number of rows in the second matrix).
Let's go back to the problem and analyze the choice 
The dimension of the first matrix is 2 x 3, because it has two rows and three columns. The second matrix has dimension 2 x 2, because it has two rows and two columns.
We can't multiply these matrices because the number of columns in the first matrix (3) is not equal to the number of rows in the second matrix (2). Thus, this product is not defined.
The answer is 
← Didn't Know|Knew It →
Simplify.

Simplify.
Tap to reveal answer
Convert the mixed numbers into improper fractions by multiplying the whole number by the denominator and adding the numerator to get 
Dividing by a fraction is the same as multiplying by its reciprocal so the problem becomes 
Convert the mixed numbers into improper fractions by multiplying the whole number by the denominator and adding the numerator to get
Dividing by a fraction is the same as multiplying by its reciprocal so the problem becomes
← Didn't Know|Knew It →
Simplify  .
.
Simplify 
Tap to reveal answer
Chenge the mixed numbers into improper fractions by multiplying the whole number by the denominator and adding the numerator to get
 .
.
Chenge the mixed numbers into improper fractions by multiplying the whole number by the denominator and adding the numerator to get

← Didn't Know|Knew It →
Find the  -intercepts for the graph given by the equation:
-intercepts for the graph given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts, we must set
-intercepts, we must set  .
.
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.



Now we must set up our two scenarios:
 and
and 
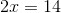 and
and 
 and
and 
To find the 

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
Now we must set up our two scenarios:

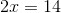

← Didn't Know|Knew It →
Solve for  .
.

Solve for 
Tap to reveal answer

Divide both sides by 3.

Consider both the negative and positive values for the absolute value term.

Subtract 2 from both sides to solve both scenarios for  .
.

Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for 
← Didn't Know|Knew It →
Solve for  :
:

Solve for 
Tap to reveal answer
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.


and

This gives us:
 and
and 

However, this question has an  outside of the absolute value expression, in this case
outside of the absolute value expression, in this case  . Thus, any negative value of
. Thus, any negative value of  will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,
will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,  is an extraneous solution, as
is an extraneous solution, as  cannot equal a negative number.
cannot equal a negative number.
Our final solution is then

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:

However, this question has an 




Our final solution is then
← Didn't Know|Knew It →

What are the possible values for  ?
?
What are the possible values for 
Tap to reveal answer
The absolute value measures the distance from zero to the given point.
In this case, since  ,
,  or
or  , as both values are twelve units away from zero.
, as both values are twelve units away from zero.
The absolute value measures the distance from zero to the given point.
In this case, since 


← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Solve:

Solve:
Tap to reveal answer
The absolute value can never be negative, so the equation is ONLY valid at zero.
The equation to solve becomes  .
.

The absolute value can never be negative, so the equation is ONLY valid at zero.
The equation to solve becomes 
← Didn't Know|Knew It →
Expression 1: 
Expression 2: 
Find the set of values for  where Expression 1 is greater than Expression 2.
where Expression 1 is greater than Expression 2.
Expression 1:
Expression 2:
Find the set of values for 
Tap to reveal answer
In finding the values for  where
where  , break the comparison of these two absolute value expressions into the four possible ways this could potentially be satisfied.
, break the comparison of these two absolute value expressions into the four possible ways this could potentially be satisfied.
The first possibility is described by the inequality:

If you think of a number line, it is evident that there is no solution to this inequality since there will never be a case where subtracting from  will lead to a greater number than adding to
will lead to a greater number than adding to  .
.
The second possibility, wherein  is negative and converted to its opposite to being an absolute value expression but
is negative and converted to its opposite to being an absolute value expression but  is positive and requires no conversion, can be represented by the inequality (where the sign is inverted due to multiplication by a negative):
is positive and requires no conversion, can be represented by the inequality (where the sign is inverted due to multiplication by a negative):

We can simplify this inequality to find that  satisfies the conditions where
satisfies the conditions where  .
.
The third possibility can be represented by the following inequality (where the sign is inverted due to multiplication by a negative):

This is again simplified to  and is redundant with the above inequality.
and is redundant with the above inequality.
The final possibility is represented by the inequality

This inequality simplifies to  . Rewriting this as
. Rewriting this as  makes it evident that this inequality is true of all real numbers. This does not provide any additional conditions on how to satisfy the original inequality.
makes it evident that this inequality is true of all real numbers. This does not provide any additional conditions on how to satisfy the original inequality.
The only possible condition that satisfies the inequality is that which arises in two of the tested cases, when  .
.
In finding the values for 

The first possibility is described by the inequality:
If you think of a number line, it is evident that there is no solution to this inequality since there will never be a case where subtracting from 

The second possibility, wherein 

We can simplify this inequality to find that 

The third possibility can be represented by the following inequality (where the sign is inverted due to multiplication by a negative):
This is again simplified to 
The final possibility is represented by the inequality
This inequality simplifies to 

The only possible condition that satisfies the inequality is that which arises in two of the tested cases, when 
← Didn't Know|Knew It →
What is the absolute value of -3?
What is the absolute value of -3?
Tap to reveal answer
The absolute value is the distance from a given number to 0. In our example, we are given -3. This number is 3 units away from 0, and thus the absolute value of -3 is 3.
If a number is negative, its absolute value will be the positive number with the same magnitude. If a number is positive, it will be its own absolute value.
The absolute value is the distance from a given number to 0. In our example, we are given -3. This number is 3 units away from 0, and thus the absolute value of -3 is 3.
If a number is negative, its absolute value will be the positive number with the same magnitude. If a number is positive, it will be its own absolute value.
← Didn't Know|Knew It →
What is the absolute value of 
What is the absolute value of
Tap to reveal answer
The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.
The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.
← Didn't Know|Knew It →




