Algebra I - Math

First, we find the slope between the two points:

and

Plug the slope and one point into the slope-intercept form to calculate the intercept:

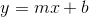
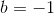
Thus the equation between the points becomes .

Since a perpendicular line has a slope that is the negative reciprocal of the original line, the new slope is . There is only one answer with the correct slope.

Two lines are parallel if they have the same slope. When a line is in standard form, the is the slope.

For the given line , the slope will be . Only one other line has a slope of :

By definition, two lines are parallel if they have the same slope. Notice that since we are given the lines in the format, and our slope is given by , it is clear that the slopes are not the same in this case, and thus the lines are not parallel.

For one equation to be parallel to another, the only requirement is that they must have the same slope. In order to figure out which answer choice is parallel to the given equation, you must first find the slope of the equation:

From the simplified equation, you can see that the slope is .

The answer choice that has the same slope is .

The formula for the length of a line is very similiar to the pythagorean theorem:

Plug in our given numbers to solve:

If B is the midpoint of AC, then AC is twice as long as AB. We are told that AB=6.

The diagram shows six units between points A and B, with B as the midpoint of segment AC. Therefore segment BC is also six units long, so line AC is twelve units long.

The formula for the length of a line is very similiar to the pythagorean theorem:

Plug in our given numbers to solve:

The formula for the length of line is the distance formula, which is very similar to the Pythagorean theorem.

Plug in the given values and solve for the length.

The midpoint of a line segment is halfway between the two values and halfway between the two values.

Mathematically, that would be the average of the coordinates: .

Plug in the values from the given points.

Now we can solve for the missing value.

The values reduce, so both values equal . Now we need to create a new equation to solve for the value.

Multiply both sides by to solve.

The formula for the length of line is the distance formula, which is very similar to the Pythagorean theorem.

Plug in the given values and solve for the length.

The formula for the length of a line, l, is the distance formula, which is very similar to the Pythagorean Theorem.

Note that the problem has already given us a value for the length of the line. That means . Plug in all of the given values and solve for the missing term.

Subtract from both sides.

Find the slope between the two points:

Next, use the slope-intercept form of the equation:

or where

So the equation becomes or in standard form .

The formula for the length of a line is very similiar to the pythagorean theorem:

Plug in our given numbers to solve:

First, calculate the slope of the line segment between the given points.

We want a line that is perpendicular to this segment and passes through its midpoint. The slope of a perpendicular line is the negative inverse. The slope of the perpendicular bisector will be .

Next, we need to find the midpoint of the segment, using the midpoint formula.

Using the midpoint and the slope, we can solve for the value of the y-intercept.

Using this value, we can write the equation for the perpendicular bisector in slope-intercept form.

Use the distance formula:

Plug in the given points:

Use the distance formula:

Substitute the given points into the formula:

The distance formula is just a reworking of the Pythagorean theorem:

Expand that.

Plug in our given values.

Let and .

The distance formula is given by .

Substitute in the given points: