How to find the area of a hexagon
ISEE Upper Level Quantitative Reasoning · Learn by Concept
Help Questions
ISEE Upper Level Quantitative Reasoning › How to find the area of a hexagon
1 - 1
1
Which is the greater quantity?
(a) The area of a regular hexagon with sidelength 1
(b) The area of an equilateral triangle with sidelength 2
(a) is greater
CORRECT
(b) is greater
(a) and (b) are equal
It is impossible to tell from the information given
Explanation
A regular hexagon with sidelength 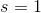


AI Study CoachYour personal study buddy
Instant TutoringConnect with a tutor now
Request a TutorGet matched with an expert
Live ClassesJoin interactive classes
Question of the DayDaily practice to build your skills
FlashcardsStudy and memorize key concepts
WorksheetsBuild custom practice quizzes
AI SolverStep-by-step problem solutions
Learn by ConceptMaster concepts step by step
Diagnostic TestsAssess your knowledge level
Practice TestsTest your skills with exam questions
GamesLearn through free games