Geometry - ISEE Upper Level Quantitative Reasoning
Card 1 of 2784
In isosceles triangle ABC, the measure of angle A is 50 degrees. Which is NOT a possible measure for angle B?
In isosceles triangle ABC, the measure of angle A is 50 degrees. Which is NOT a possible measure for angle B?
Tap to reveal answer
If angle A is one of the base angles, then the other base angle must measure 50 degrees. Since 50 + 50 + x = 180 means x = 80, the vertex angle must measure 80 degrees.
If angle A is the vertex angle, the two base angles must be equal. Since 50 + x + x = 180 means x = 65, the two base angles must measure 65 degrees.
The only number given that is not possible is 95 degrees.
If angle A is one of the base angles, then the other base angle must measure 50 degrees. Since 50 + 50 + x = 180 means x = 80, the vertex angle must measure 80 degrees.
If angle A is the vertex angle, the two base angles must be equal. Since 50 + x + x = 180 means x = 65, the two base angles must measure 65 degrees.
The only number given that is not possible is 95 degrees.
← Didn't Know|Knew It →
Let the three angles of a triangle measure  ,
,  , and
, and  .
.
Which of the following expressions is equal to  ?
?
Let the three angles of a triangle measure 


Which of the following expressions is equal to 
Tap to reveal answer
The sum of the measures of the angles of a triangle is  , so simplify and solve for
, so simplify and solve for  in the equation:
in the equation:





The sum of the measures of the angles of a triangle is 

← Didn't Know|Knew It →
The angles of a triangle measure  ,
,  , and
, and  . Give
. Give  in terms of
in terms of  .
.
The angles of a triangle measure 




Tap to reveal answer
The sum of the measures of three angles of a triangle is  , so we can set up the equation:
, so we can set up the equation:

We can simplify and solve for  :
:



The sum of the measures of three angles of a triangle is 
We can simplify and solve for 
← Didn't Know|Knew It →
Which of the following is true about a triangle with two angles that measure  each?
each?
Which of the following is true about a triangle with two angles that measure 
Tap to reveal answer
The measures of the angles of a triangle total  , so if two angles measure
, so if two angles measure  and we call
and we call  the measure of the third, then
the measure of the third, then




This makes the triangle obtuse.
Also, since the triangle has two congruent angles (the  angles), the triangle is also isosceles.
angles), the triangle is also isosceles.
The measures of the angles of a triangle total 


This makes the triangle obtuse.
Also, since the triangle has two congruent angles (the 
← Didn't Know|Knew It →
You are given two triangles,  and
and  .
.
 ,
,  is an acute angle, and
is an acute angle, and  is a right angle.
is a right angle.
Which quantity is greater?
(a) 
(b) 
You are given two triangles, 




Which quantity is greater?
(a)
(b)
Tap to reveal answer
We invoke the SAS Inequality Theorem, which states that, given two triangles  and
and  , with
, with  ,
,  ( the included angles), then
( the included angles), then  - that is, the side opposite the greater angle has the greater length. Since
- that is, the side opposite the greater angle has the greater length. Since  is an acute angle, and
is an acute angle, and  is a right angle, we have just this situation. This makes (b) the greater.
is a right angle, we have just this situation. This makes (b) the greater.
We invoke the SAS Inequality Theorem, which states that, given two triangles 






← Didn't Know|Knew It →

Refer to the above figure. Which is the greater quantity?
(a) 
(b) 

Refer to the above figure. Which is the greater quantity?
(a)
(b)
Tap to reveal answer
The Triangle Exterior-Angle Theorem states that the measure of an exterior angle is equal to the sum of its remote interior angles. Therefore,
 ,
,
making the quantities equal.
The Triangle Exterior-Angle Theorem states that the measure of an exterior angle is equal to the sum of its remote interior angles. Therefore,

making the quantities equal.
← Didn't Know|Knew It →

Note: Figure NOT drawn to scale.
Refer to the above figure. Which is the greater quantity?
(a) 
(b) 

Note: Figure NOT drawn to scale.
Refer to the above figure. Which is the greater quantity?
(a)
(b)
Tap to reveal answer
(a) The measures of the angles of a linear pair total 180, so:




(b) The Triangle Exterior-Angle Theorem states that the measure of an exterior angle is equal to the sum of its remote interior angles. Therefore,  .
.
Therefore (a) is the greater quantity.
(a) The measures of the angles of a linear pair total 180, so:
(b) The Triangle Exterior-Angle Theorem states that the measure of an exterior angle is equal to the sum of its remote interior angles. Therefore, 
Therefore (a) is the greater quantity.
← Didn't Know|Knew It →

Note: Figure NOT drawn to scale.
Refer to the above figure. Which is the greater quantity?
(a) 
(b) 

Note: Figure NOT drawn to scale.
Refer to the above figure. Which is the greater quantity?
(a)
(b)
Tap to reveal answer
The two angles at bottom are marked as congruent. Each of these two angles forms a linear pair with a  angle, so it is supplementary to that angle, making its measure
angle, so it is supplementary to that angle, making its measure  . Therefore, the other marked angle also measures
. Therefore, the other marked angle also measures  .
.
The sum of the measures of the interior angles of a triangle is  , so:
, so:




The quantities are equal.
The two angles at bottom are marked as congruent. Each of these two angles forms a linear pair with a 


The sum of the measures of the interior angles of a triangle is 
The quantities are equal.
← Didn't Know|Knew It →
 is equilateral;
is equilateral;  is isosceles
is isosceles

Which is the greater quantity?
(a) 
(b) 


Which is the greater quantity?
(a)
(b)
Tap to reveal answer
 is equilateral, so
is equilateral, so
 .
.
In  , we are given that
, we are given that
 .
.
Since the triangles have two pair of congruent sides, the third side with the greater length is opposite the angle of greater measure. Therefore,
 .
.
Since  is an angle of an equilateral triangle, its measure is
is an angle of an equilateral triangle, its measure is  , so
, so  .
.


In 

Since the triangles have two pair of congruent sides, the third side with the greater length is opposite the angle of greater measure. Therefore,

Since 


← Didn't Know|Knew It →



Which is the greater quantity?
(a) 
(b) 
Which is the greater quantity?
(a)
(b)
Tap to reveal answer
Corresponding angles of similar triangles are congruent, so, since  , it follows that
, it follows that

By similarity,  and
and  , and we are given that
, and we are given that  , so
, so

Also,




 ,
,
and  .
.
Corresponding angles of similar triangles are congruent, so, since 
By similarity, 


Also,

and 
← Didn't Know|Knew It →

Refer to the above figure. Which is the greater quantity?
(a) 
(b) 

Refer to the above figure. Which is the greater quantity?
(a)
(b)
Tap to reveal answer
Extend  as seen in the figure below:
as seen in the figure below:

The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles; specifically,
 ,
,
and

However,  , so, by substitution,
, so, by substitution,

Extend 

The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles; specifically,

and
However, 
← Didn't Know|Knew It →
Given:  .
.  . Which is the greater quantity?
. Which is the greater quantity?
(a) 
(b) 
Given: 

(a)
(b)
Tap to reveal answer
Below is the referenced triangle along with  , an equilateral triangle with sides of length 10:
, an equilateral triangle with sides of length 10:

As an angle of an equilateral triangle,  has measure
has measure  . Applying the Side-Side-Side Inequality Theorem, since
. Applying the Side-Side-Side Inequality Theorem, since  ,
,  , and
, and  , it follows that
, it follows that  , so
, so  .
.
Also, since  , by the Isosceles Triangle Theorem,
, by the Isosceles Triangle Theorem,  . Since
. Since  , and the sum of the measures of the angles of a triangle is
, and the sum of the measures of the angles of a triangle is  , it follows that
, it follows that

Substituting and solving:



 .
.
Below is the referenced triangle along with 

As an angle of an equilateral triangle, 






Also, since 



Substituting and solving:

← Didn't Know|Knew It →
The perimeter of a square is one yard. Which is the greater quantity?
(a) The area of the square
(b)  square foot
square foot
The perimeter of a square is one yard. Which is the greater quantity?
(a) The area of the square
(b) 
Tap to reveal answer
One yard is equal to three feet, so the length of one side of a square with this perimeter is  feet. The area of the square is
feet. The area of the square is  square feet.
square feet.  , making (a) greater.
, making (a) greater.
One yard is equal to three feet, so the length of one side of a square with this perimeter is 


← Didn't Know|Knew It →

Note: Figure NOT drawn to scale.
Refer to the above figure.
Which is the greater quantity?
(a) 
(b) 

Note: Figure NOT drawn to scale.
Refer to the above figure.
Which is the greater quantity?
(a)
(b)
Tap to reveal answer
Since the shorter leg of the right triangle is half the hypotenuse, the triangle is a  triangle, with the
triangle, with the  angle opposite the shorter leg. That makes
angle opposite the shorter leg. That makes  .
.
Since the shorter leg of the right triangle is half the hypotenuse, the triangle is a 


← Didn't Know|Knew It →
 is an equilateral triangle. Points
is an equilateral triangle. Points 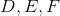 are the midpoints of
are the midpoints of  , respectively.
, respectively.  is constructed.
is constructed.
Which is the greater quantity?
(a) The area of 
(b) Twice the area of 

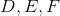


Which is the greater quantity?
(a) The area of
(b) Twice the area of
Tap to reveal answer
If segments are constructed in which the endpoints form the midpoints of the sides of a triangle, then four triangles, congruent to each other and similar to the larger triangle, are formed. Therefore, one of these triangles - specifically,  - would have one-fourth the area of
- would have one-fourth the area of 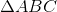 . This means
. This means  has more than twice the area of
has more than twice the area of  .
.
Note that the fact that the triangle is equilateral is irrelevant.
If segments are constructed in which the endpoints form the midpoints of the sides of a triangle, then four triangles, congruent to each other and similar to the larger triangle, are formed. Therefore, one of these triangles - specifically, 
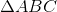


Note that the fact that the triangle is equilateral is irrelevant.
← Didn't Know|Knew It →
Which of the following could be the three sidelengths of an equilateral triangle?
Which of the following could be the three sidelengths of an equilateral triangle?
Tap to reveal answer
By definition, an equilateral triangle has three sides of equal length. We can identify the equilateral triangle by converting the given sidelengths to the same units and comparing them.
We can eliminate the following by showing that at least two sidelengths differ.

2 yards =  feet.
feet.
Two sides have lengths 6 feet and 7 feet, so we can eliminate this choice.

4 feet =  inches
inches
Two sides have lengths 48 inches and 50 inches, so we can eliminate this choice.

5 feet =  inches
inches
Two sides have lengths 48 inches and 60 inches, so we can eliminate this choice.

 yards =
yards =  feet
feet
Two sides have lengths 4 feet and 5 feet, so we can eliminate this choice.

 yards =
yards =  feet =
feet =  inches
inches
All three sides have the same length, making this the triangle equilateral. This choice is correct.
By definition, an equilateral triangle has three sides of equal length. We can identify the equilateral triangle by converting the given sidelengths to the same units and comparing them.
We can eliminate the following by showing that at least two sidelengths differ.
2 yards = 
Two sides have lengths 6 feet and 7 feet, so we can eliminate this choice.
4 feet = 
Two sides have lengths 48 inches and 50 inches, so we can eliminate this choice.
5 feet = 
Two sides have lengths 48 inches and 60 inches, so we can eliminate this choice.


Two sides have lengths 4 feet and 5 feet, so we can eliminate this choice.



All three sides have the same length, making this the triangle equilateral. This choice is correct.
← Didn't Know|Knew It →
Right triangle  has right angle
has right angle  .
.

Which is the greater quantity?
(a) 
(b) 
Right triangle 

Which is the greater quantity?
(a)
(b)
Tap to reveal answer
The degree measures of the acute angles of a right triangle total 90, so we solve for  in the following equation:
in the following equation:






(a) 
(b) 

The degree measures of the acute angles of a right triangle total 90, so we solve for 
(a)
(b)
← Didn't Know|Knew It →

 is a right angle.
is a right angle.
Which is the greater quantity?
(a) 
(b) 

Which is the greater quantity?
(a)
(b)
Tap to reveal answer
Corresponding angles of similar triangles are congruent, so, since  , and
, and  is right, it follows that
is right, it follows that

 is a right angle of a right triangle
is a right angle of a right triangle  . The other two angles must be acute - that is, with measure less than
. The other two angles must be acute - that is, with measure less than  - so
- so  .
.
Corresponding angles of similar triangles are congruent, so, since 





← Didn't Know|Knew It →
 is inscribed in a circle.
is inscribed in a circle.  is a right angle, and
is a right angle, and  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
Tap to reveal answer
The figure referenced is below:

 has measure
has measure  , so its corresponding minor arc,
, so its corresponding minor arc,  , has measure
, has measure  . The inscribed angle that intercepts this arc, which is
. The inscribed angle that intercepts this arc, which is  , has measure half this, or
, has measure half this, or  . Since
. Since  is a right angle, the other acute angle,
is a right angle, the other acute angle,  , has measure
, has measure

Therefore,  .
.
The figure referenced is below:









Therefore, 
← Didn't Know|Knew It →
Consider a triangle,  , in which
, in which  ,
,  , and
, and  . Which is the greater number?
. Which is the greater number?
(a) The measure of  in degrees
in degrees
(b) 
Consider a triangle, 



(a) The measure of 
(b)
Tap to reveal answer
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities  and
and 


 , so
, so  is right, with the right angle opposite longest side
is right, with the right angle opposite longest side  . Thus,
. Thus,  is right and has degree measure 90.
is right and has degree measure 90.
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities 




← Didn't Know|Knew It →