Geometry - HSPT Math

Card 0 of 2400

Question

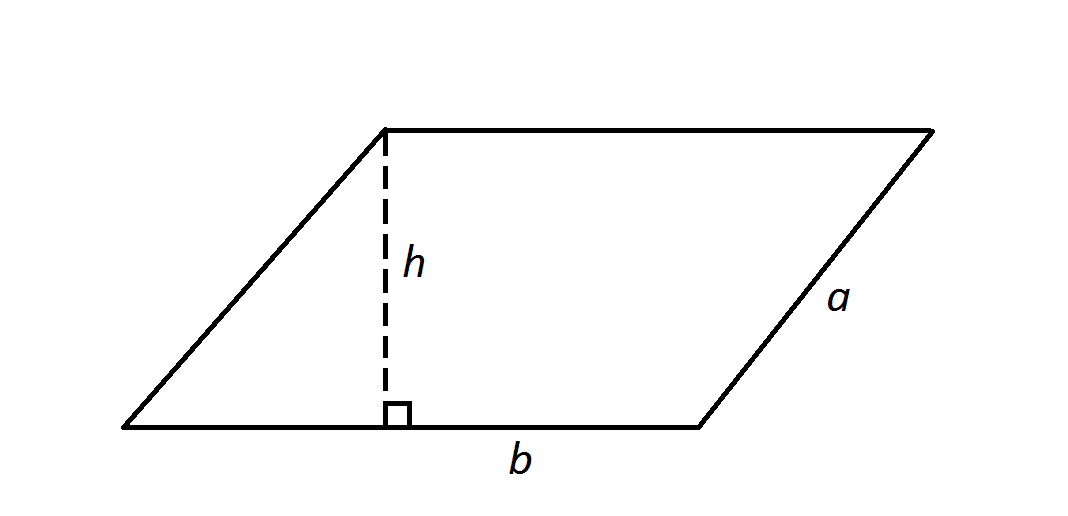
Note: Figure NOT drawn to scale.

$a = 18; \textrm{in} ,b=26; \textrm{in},h=12; \textrm{in}$ , where and represent side lengths of the parallelogram and represents the height.

Find the perimeter of the parallelogram in the diagram.

Answer

The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes

.

Note that the height is irrelevant to the answer.

Compare your answer with the correct one above

Question

Assume π = 3.14

A man would like to put a circular whirlpool in his backyard. He would like the whirlpool to be six feet wide. His backyard is 8 feet long by 7 feet wide. By state regulation, in order to put a whirlpool in a backyard space, the space must be 1.5 times bigger than the pool. Can the man legally install the whirlpool?

Answer

If you answered that the whirlpool’s area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.

If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.

If you answered that the area of the backyard was smaller than the area of the whirlpool, you did not calculate area correctly.

And if you thought the area of the backyard was 30 feet, you found the perimeter of the backyard, not the area.

The correct answer is that the area of the whirlpool is 28.26 feet and, when multiplied by 1.5 = 42.39, which is smaller than the area of the backyard, which is 56 square feet.

Compare your answer with the correct one above

Question

A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.25 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 44 in.?

Answer

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in2.

Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr2 or π * 442 = 1936π in2. Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.

Compare your answer with the correct one above

Question

Mary has a decorative plate with a diameter of ten inches. She places the plate on a rectangular placemat with a length of 18 inches and a width of 12 inches. How much of the placemat is visible?

Answer

First we will calculate the total area of the placemat:

$A=l\times w= 18\times 12= 216\hspace{1 mm}inches^2$

Next we will calculate the area of the circular place

$A=\pi r^2$

And

$d=2r=10$

So

$r=5\hspace{1 mm}inches$

$A=\pi r^2=\pi (5^2)=25\pi\hspace{1 mm}inches^2$

We will subtract the area of the plate from the total area

$216-25\pi\hspace{1 mm}inches^2$

Compare your answer with the correct one above

Question

What is the area of a circle with a radius of 10?

Answer

The formula for the area of a circle is $\dpi{100} \pi r^{2}$

$\dpi{100} \pi r^{2}= \pi (10)^{2}=100\pi$

Compare your answer with the correct one above

Question

Allen was running around the park when he lost his keys. He was running around aimlessly for the past 30 minutes. When he checked 10 minutes ago, he still had his keys. Allen guesses that he has been running at about 3m/s.

If Allen can check 1 square kilometer per hour, what is the longest it will take him to find his keys?

Answer

Allen has been running for 10 minutes since he lost his keys at 3m/s. This gives us a maximum distance of from his current location. If we move 1800m in all directions, this gives us a circle with radius of 1800m. The area of this circle is

$1800^2\pi \approx 10,178,760m^2$

Our answer, however, is asked for in kilometers. 1800m=1.8km, so our actual area will be $\frac{10,178,760}{1,000,000} = 10.2$ square kilometers. Since he can search 1 per hour, it will take him at most 10.2 hours to find his keys.

Compare your answer with the correct one above

Question

What is the area of a circle with a radius of 7?

Answer

To find the area of a circle you must plug the radius into in the following equation $A=\pi(r^{2})$

In this case the radius is 7 so we plug it into to get $7^{2}=49$

We then multiply it by pi to get our answer $A=49\pi$

Compare your answer with the correct one above

Question

What is the area of a square with a side length of 8?

Answer

To solve this question you must know the formula for the area of a rectangle.

The formula is

In this case the rectangle is a square so we can plug in the side length for both base and height to yield

Perform the multiplication to arrive at the answer of

Compare your answer with the correct one above

Question

Refer to the above diagram, which shows an equilateral triangle with one vertex at the center of a circle and two vertices on the circle.

What percent of the circle (nearest whole number) is covered by the triangle?

Answer

Let be the radius of the circle. The area of the circle is

$A_{1} = \pi r^{2}$

is also the sidelength of the equilateral triangle. The area of the triangle is

$A_{2} = \frac{\sqrt{3}}{4} ; r^{2}$

The percent of the circle covered by the triangle is:

$\frac{A_{2} }{A_{1}} \cdot 100= \frac{\frac{\sqrt{3}}{4}r^{2}}{\pi r^{2}}\cdot 100 = \frac{100 \sqrt{3}}{4 \pi } \approx 14$

Compare your answer with the correct one above

Question

I have a hollow cube with 3” sides suspended inside a larger cube of 9” sides. If I fill the larger cube with water and the hollow cube remains empty yet suspended inside, what volume of water was used to fill the larger cube?

Answer

Determine the volume of both cubes and then subtract the smaller from the larger. The large cube volume is 9” * 9” * 9” = 729 in3 and the small cube is 3” * 3” * 3” = 27 in3. The difference is 702 in3.

Compare your answer with the correct one above

Question

A cube weighs 5 pounds. How much will a different cube of the same material weigh if the sides are 3 times as long?

Answer

A cube that has three times as long sides is 3x3x3=27 times bigger than the original. Therefore, the answer is 5x27= 135.

Compare your answer with the correct one above

Question

The volume of a cylinder is 36π. If the cylinder’s height is 4, what is the cylinder’s diameter?

Answer

Volume of a cylinder? V = πr2h. Rewritten as a diameter equation, this is:

V = π(d/2)2h = πd2h/4

Sub in h and V: 36p = πd2(4)/4 so 36p = πd2

Thus d = 6

Compare your answer with the correct one above

Question

What is the area of a triangle with a side lengths of 5?

Answer

The area of a triangle is found with the equation

$a=\frac{1}{2}b h$ .

Since we do not have the height, we cannot answer the question.

Compare your answer with the correct one above

Question

A room has dimensions of 18ft by 15ft by 9ft. The last dimension is the height of the room. It has one door that is 3ft by 7ft and two windows, each 2ft by 5ft. There is no trim to the floor, wall, doors, or windows. What is the total exposed wall space?

Answer

If broken down into parts, this is an easy problem. It is first necessary to isolate the dimensions of the walls. If the room is 9 ft high, we know 18 x 15 designates the area of the floor and ceiling. Based on this, we know that the room has the following dimensions for the walls: 18 x 9 and 15 x 9. Since there are two of each, we can calculate the total area of walls - ignoring doors and windows - by doubling the sum of these two areas:

2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 ft2

Now, we merely need to calculate the area "taken out" of the walls:

For the door: 3 * 7 = 21 ft2

For the windows: 2 * (2 * 5) = 20 ft2

The total wall space is therefore: 594 – 21 – 20 = 553 ft2

Compare your answer with the correct one above

Question

You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?

Answer

The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:

The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so

$5\times 1.3 =6.5\hspace{1 mm}miles$

Compare your answer with the correct one above

Question

Which of the following points will you find on the -axis?

Answer

A point is located on the -axis if and only if it has -coordinate (first coordinate) 0. Of the five choices, only fits that description.

Compare your answer with the correct one above

Question

Which of the following is a vertex of the square?

Answer

The coordinates of a point are determined by the distance from the origin. The first point in the ordered pair is the number of units to the left or right of the origin. Negative numbers indicate the number of units to the left while positive numbers indicate the number of units to the right. The second number indicates the number of units above or below the origin. Positive numbers indicate the number of units above while negative numbrs indicate the number of units below the origin. The vertices of the square are:
$\small (-1,2); (-1,4); (1,2); (-1,4)$

Compare your answer with the correct one above

Question

Which of the following points is on the -axis?

Answer

A point is located on the -axis if and only if it has a -coordinate equal to zero. So the answer is .

Compare your answer with the correct one above

Question

Billy set up a ramp for his toy cars. He did this by taking a wooden plank and putting one end on top of a brick that was 3 inches high. He then put the other end on top of a box that was 9 inches high. The bricks were 18 inches apart. What is the slope of the plank?

Answer

The value of the slope (m) is rise over run, and can be calculated with the formula below:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The coordinates of the first end of the plank would be (0,3), given that this is the starting point of the plank (so x would be 0), and y would be 3 since the brick is 3 inches tall.

The coordinates of the second end of the plank would be (18,9) since the plank is 18 inches long (so x would be 18) and y would be 9 since the box was 9 inches tall at the other end.

From this information we know that we can assign the following coordinates for the equation:

$\left(x_{1},y_{1}\right) = (0,3)$ and $(x_{2}, y_{2})= (18,9)$

Below is the solution we would get from plugging this information into the equation for slope:

$m = \frac{9-3}{18-0}}$

This reduces to $\frac{6}{18} =\frac{1}{3}$

Compare your answer with the correct one above

Question

A deer walks in a straight line for 8 hours. At the end of its journey, the deer is 30 miles north and 40 miles east of where it began. What was the average speed of the deer?

Answer

To find the speed of the deer, you must have the distance traveled and the time.

The distance is found using the Pythagorean Theorem:

$C = {\sqrt{A^2+ B^2}}$

$C = \sqrt{30^2 + 40^2}$

$C = \sqrt{2500} = 50$

The answer must be in miles per hour so the total miles are divided by the hours to get the final answer:

$\frac{miles}{hour} = \frac{50}{8} = 6.25 mph$

Compare your answer with the correct one above

Tap the card to reveal the answer