Concepts - HSPT Math
Card 0 of 8060
Simplify the following expression: (–4)(2)(–1)(–3)
Simplify the following expression: (–4)(2)(–1)(–3)
First, we multiply –4 and 2. A negative and a positive number multiplied together give us a negative number, so (–4)(2) = –8. A negative times a negative is a positive so (–8)(–1) = 8. (8)(–3) = –24.
First, we multiply –4 and 2. A negative and a positive number multiplied together give us a negative number, so (–4)(2) = –8. A negative times a negative is a positive so (–8)(–1) = 8. (8)(–3) = –24.
Compare your answer with the correct one above
What is the equivalent of 
%?
What is the equivalent of
Divide: 
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is the equivalent of 
%?
What is the equivalent of
Divide: 
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is the equivalent of 
%?
What is the equivalent of
Divide: 
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is 
% off of 
?
What is
First multiply: 
Then, subtract: 
Answer: 
First multiply:
Then, subtract:
Answer:
Compare your answer with the correct one above
What is 
% off of 
?
What is
First multiply: 
Then, subtract: 
Answer: 
First multiply:
Then, subtract:
Answer:
Compare your answer with the correct one above
What is 
% off of 
?
What is
First multiply: 
Then, subtract: 
Answer: 
First multiply:
Then, subtract:
Answer:
Compare your answer with the correct one above
What is the equivalent to 
?
What is the equivalent to
Divide: 
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is the equivalent of 
?
What is the equivalent of
Divide: 
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is the equivalent to 
?
What is the equivalent to
Divide:
Answer: 
Divide:
Answer:
Compare your answer with the correct one above
What is 
off of 
?
What is
First, multiply: 
Then, subtract: 
Answer: 
First, multiply:
Then, subtract:
Answer:
Compare your answer with the correct one above
If a = –2 and b = –3, then evaluate a3 + b2
If a = –2 and b = –3, then evaluate a3 + b2
When multiplying negative numbers, we get a negative answer if there are an odd number of negative numbers being multiplied. We get a positive answer if there are an even number of negative numbers being multiplied.
a3 + b2 becomes (–2)3 + (–3)2 which equals –8 + 9 = 1
When multiplying negative numbers, we get a negative answer if there are an odd number of negative numbers being multiplied. We get a positive answer if there are an even number of negative numbers being multiplied.
a3 + b2 becomes (–2)3 + (–3)2 which equals –8 + 9 = 1
Compare your answer with the correct one above
What is 1 + (–1) – (–3) + 4 ?
What is 1 + (–1) – (–3) + 4 ?
You simplify the expression to be 1 – 1 + 3 + 4 = 7
You simplify the expression to be 1 – 1 + 3 + 4 = 7
Compare your answer with the correct one above
Evaluate:
–3 * –7
Evaluate:
–3 * –7
Multiplying a negative number and another negative number makes the product positive.
Multiplying a negative number and another negative number makes the product positive.
Compare your answer with the correct one above
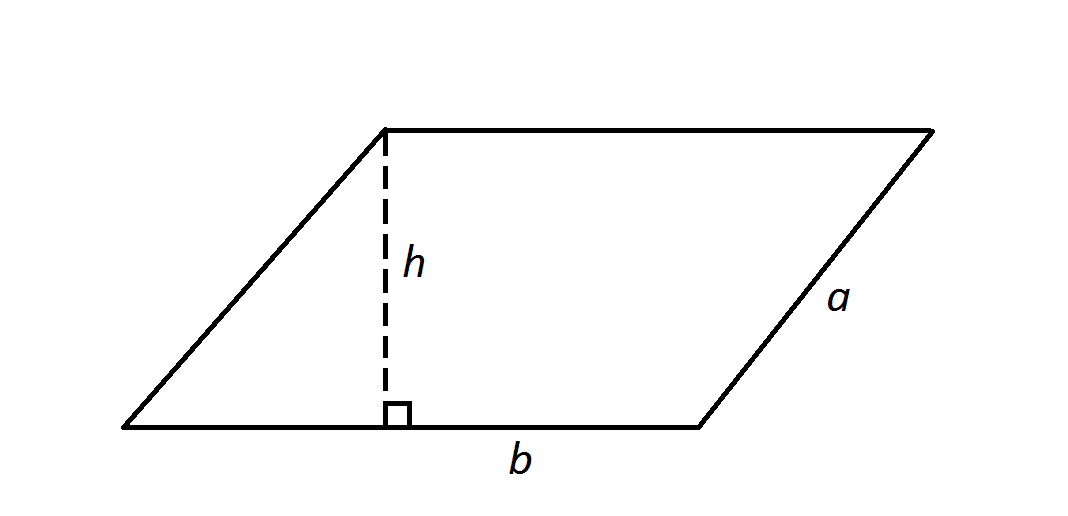
Note: Figure NOT drawn to scale.
, where 
and 
represent side lengths of the parallelogram and 
represents the height.
Find the perimeter of the parallelogram in the diagram.
Note: Figure NOT drawn to scale.
Find the perimeter of the parallelogram in the diagram.
The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes
.
Note that the height 
is irrelevant to the answer.
The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes
Note that the height
Compare your answer with the correct one above
Assume π = 3.14
A man would like to put a circular whirlpool in his backyard. He would like the whirlpool to be six feet wide. His backyard is 8 feet long by 7 feet wide. By state regulation, in order to put a whirlpool in a backyard space, the space must be 1.5 times bigger than the pool. Can the man legally install the whirlpool?
Assume π = 3.14
A man would like to put a circular whirlpool in his backyard. He would like the whirlpool to be six feet wide. His backyard is 8 feet long by 7 feet wide. By state regulation, in order to put a whirlpool in a backyard space, the space must be 1.5 times bigger than the pool. Can the man legally install the whirlpool?
If you answered that the whirlpool’s area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.
If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.
If you answered that the area of the backyard was smaller than the area of the whirlpool, you did not calculate area correctly.
And if you thought the area of the backyard was 30 feet, you found the perimeter of the backyard, not the area.
The correct answer is that the area of the whirlpool is 28.26 feet and, when multiplied by 1.5 = 42.39, which is smaller than the area of the backyard, which is 56 square feet.
If you answered that the whirlpool’s area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.
If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.
If you answered that the area of the backyard was smaller than the area of the whirlpool, you did not calculate area correctly.
And if you thought the area of the backyard was 30 feet, you found the perimeter of the backyard, not the area.
The correct answer is that the area of the whirlpool is 28.26 feet and, when multiplied by 1.5 = 42.39, which is smaller than the area of the backyard, which is 56 square feet.
Compare your answer with the correct one above
A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.25 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 44 in.?
A manufacturer makes wooden circles out of square blocks of wood. If the wood costs $0.25 per square inch, what is the minimum waste cost possible for cutting a circle with a radius of 44 in.?
The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in2.
Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr2 or π * 442 = 1936π in2. Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.
The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in2.
Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr2 or π * 442 = 1936π in2. Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.
Compare your answer with the correct one above
Mary has a decorative plate with a diameter of ten inches. She places the plate on a rectangular placemat with a length of 18 inches and a width of 12 inches. How much of the placemat is visible?
Mary has a decorative plate with a diameter of ten inches. She places the plate on a rectangular placemat with a length of 18 inches and a width of 12 inches. How much of the placemat is visible?
First we will calculate the total area of the placemat:
Next we will calculate the area of the circular place
And
So
We will subtract the area of the plate from the total area
First we will calculate the total area of the placemat:
Next we will calculate the area of the circular place
And
So
We will subtract the area of the plate from the total area
Compare your answer with the correct one above
What is the area of a circle with a radius of 10?
What is the area of a circle with a radius of 10?
The formula for the area of a circle is 
The formula for the area of a circle is
Compare your answer with the correct one above
Allen was running around the park when he lost his keys. He was running around aimlessly for the past 30 minutes. When he checked 10 minutes ago, he still had his keys. Allen guesses that he has been running at about 3m/s.
If Allen can check 1 square kilometer per hour, what is the longest it will take him to find his keys?
Allen was running around the park when he lost his keys. He was running around aimlessly for the past 30 minutes. When he checked 10 minutes ago, he still had his keys. Allen guesses that he has been running at about 3m/s.
If Allen can check 1 square kilometer per hour, what is the longest it will take him to find his keys?
Allen has been running for 10 minutes since he lost his keys at 3m/s. This gives us a maximum distance of 
from his current location. If we move 1800m in all directions, this gives us a circle with radius of 1800m. The area of this circle is
Our answer, however, is asked for in kilometers. 1800m=1.8km, so our actual area will be 
square kilometers. Since he can search 1 per hour, it will take him at most 10.2 hours to find his keys.
Allen has been running for 10 minutes since he lost his keys at 3m/s. This gives us a maximum distance of
Our answer, however, is asked for in kilometers. 1800m=1.8km, so our actual area will be
Compare your answer with the correct one above