Electric Circuits - Physics

The power in a circuit is equal to the current times the voltage.

We often think of current flowing from the top of the battery to the bottom of the battery. The top of the battery has a higher electrical potential than the bottom of the battery and is associated as being positive. Charges interact in such a way where like charges repel and opposite charges attract. Since we think of the charges traveling away from the positive end of the battery and toward the negative end of the battery, this would model the motion of a positive charge (away from positive and toward negative). Since it is not protons that move through the circuit, but rather electrons. It is more accurate to describe the flow of electrons from the negative side of the battery to the positive side.

Decrease to one half its original value

The equation for Power is

According to Ohm’s Law

We can rearrange this equation for current as this is what is changing in our circuit.

We can then substitute this back into the power equation.

If we have the original value

and our second value

We can rearrange both for the voltage and set them equal to each other

,

We know that

So we can substitute this value in

And solve for

Therefore the power would be cut in half.

When plugin objects into a single circuit, these objects are connected in parallel as each one will receive the 120V from the electrical outlet. However, as additional objects are added, the current is thereby increased. Circuit breakers are designed to trip once the current reaches a maximum load and shuts down the circuit to protect the wires, and the devices that are plugged into the circuit as high current can damage these devices.

We first need to determine the current coming through the bulb. We can use Ohm’s law to determine this.

Current by definition is the amount of charge per unit time.

We are looking at the number of electrons in one minute which is 60 seconds.

We now know the amount of charge passing through in 60 seconds. We know that the charge of the electron is . We can use this to figure out how many electrons are going through.

Electricity travels from the point of highest potential to the lowest potential. We measure the difference between these two potentials as the voltage. Since both of the birds' feet are on the wire, both feet have the same potential. However, if the ladder touches the power line and the bottom of the ladder is on the ground, there is a much higher potential difference (as the ground is at 0 potential). Therefore the electricity will travel down the ladder!

It's kind of like when you turn on the faucet; the water doesn't have to travel from the water tower to your house before it starts flowing. Similarly, the electrons are always in the circuit. Once the switch is turned on, there is a voltage difference present, which is what then pushes these electrons through the circuit (like turning on the faucet).

By definition, each branch of a parallel circuit will have the same voltage. The current, however, may be split between branches in inequal amounts. In contrast, a series circuit will carry a constant current throughout the circuit, but voltage may differ between elements.

Resistance and capacitance are dependent on the elements present in a given circuit, so no claims can be made. Power is similarly dependent on the elements present in a specific circuit.

In series, the equivalent resistance is equal to the sum of each individual resistance. In parallel, the inverse of equivalent resistance is equal to the sum of the inverses of each individual resistance.

We can calculate these two values, and then find the difference between them.

Find the difference:

To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.

Now we can add this resistor to the 4 Ohm resistor as they are in series.

We can now determine the current coming out of the battery using Ohm’s Law.

Rearrange to solve for current.

The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.

Kirchoff’s loop law states that the sum of the voltage around a loop must equal zero. In other words, the voltage that is being provided by the batteries in the circuit must equal the voltage being used by the objects in the circuit. Voltage is a measure of the potential difference, or energy within the circuit. In other words, the battery does a certain amount of work and provides energy to the circuit which is then used by all the parts of the circuit. Therefore this is an example of conservation of energy.

Kirchoff’s loop rules states the sum of the current going into and out of the junction must equal 0. In other words, the current going in must equal the current going on. Current is a measure of the flow of charge. Therefore, this law is conservation of charge as the number of electrons going into a junction must equal the number of electrons flowing out.

Current is defined as the amount of charge that passes through a specific area of a wire in a specific interval of time. It is measured in Amps which are Coulombs per second.

A series circuit has the same current running through each component, though the voltage across each component may vary. In contrast, a parallel circuit will carry a constant voltage in each branch and the current may be split in inequal amounts between branches.

Resistance and capacitance are dependent on the elements present in a given circuit, so no claims can be made. Power is similarly dependent on the elements present in a specific circuit.

In basic resistors, energy lost due to resistance is converted into heat. In some cases, other conversions also take place (such as generation of light in a lightbulb), but heat is still dissipated along with any alternative conversations. Lightbulbs, batteries, and other types of resistors will become hot as current passes through them.

The standard equation for power is:

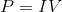
We are given only current and reistance, meaning we must manipulate this equation so that only those variables are present. To do this, we can substitute Ohm's law for voltage.

Now we have an equation for power that uses only current and resistance. Plug in the values given in the question to find the final answer.

To begin, let us start with the resistor and the resistor that are in parallel. In parallel we can add resistors through the equation

This new resistor is now in series with the two 4Ω resistors. In series we can just add these resistors up.

This new resistor is now in parallel with the resistor. In parallel we can add resistors through the equation

This new resistor is now in series with the and resistor. In series we can just add these resistors up.

Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.

Rearrange to solve for current.

One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.

We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.

Using Ohm’s Law we can determine the voltage for each of these two resistors.

We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.

To begin, let us start with the resistor and the resistor that are in parallel. In parallel we can add resistors through the equation

This new resistor is now in series with the two resistors. In series we can just add these resistors up.

This new resistor is now in parallel with the resistor. In parallel we can add resistors through the equation

This new resistor is now in series with the and resistor. In series we can just add these resistors up.

Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.

Rearrange to solve for current.

One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.

We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.

Using Ohm’s Law we can determine the voltage for each of these two resistors.

We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.

Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of junction must equal 0.

We have flowing in from the resistor and flowing out to go through the resistor.

So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.

Now let’s add this to our chart.

We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.

We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.

To begin, let us start with the resistor and the resistor that are in parallel. In parallel we can add resistors through the equation

This new resistor is now in series with the two resistors. In series we can just add these resistors up.

This new resistor is now in parallel with the resistor. In parallel we can add resistors through the equation

This new resistor is now in series with the and resistor. In series we can just add these resistors up.

Now that we have the equivalent resistance of the circuit. We can now determine the current flowing out of the battery.

Rearrange to solve for current.

One of the best ways to work through a problem like this is to create a V= IR chart for all the components of the circuit.

We know that the current that is flowing out of the battery is the current that is flowing through both by 5 and 3 Ohm resistors since all of these are in series. So we can put this information into our chart.

Using Ohm’s Law we can determine the voltage for each of these two resistors.

We can now use Kirchoff’s loop law through the loop of the 5, 3, and 14 Ohm resistor to determine the voltage that is traveling through the 14 Ohm resistor.

We can now use Ohm’s law and our voltage to determine the current going through the 14 Ohm resistor.

We can now add this information to our chart.

Next we can analyze the current in the Junction between the 5, 14 and 4 Ohm resistors. Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.

We have 4A flowing in from the 5 Ohm resistor and 1A flowing out to go through the 14 Ohm resistor.

So the current going through the 4 Ohm resistor is 3 amps. This will be the same for both 4 ohm resistors as both have the same current going into and out of the junctions near them. We can then use this to determine the voltage drop across each of the resistors.

Now let’s add this to our chart.

We can now use Kirchoff’s loop law to determine the voltage across the 10 Ohm resistor. Let’s analyze the loop that goes from the 5, to the 4 to the 10 back through the 4 and then through 3 Ohm resistor.

We can now use Ohm’s Law to determine the current through the 10 Ohm resistor.

We can now add this information to our chart.

We can now analyze the junction between the 4, 10 and 15 Ohm resistor.

Kirchoff’s laws state that the sum of the current flowing in and out of the junction must equal 0.

We have 2A flowing in from the 4 Ohm resistor and 1.2A flowing out to go through the 10 Ohm resistor.

To begin we need to simplify the circuit to get the equivalent resistance. Let’s start with the 3 and 6 Ohm resistors in parallel.

Now we can add this resistor to the 4 Ohm resistor as they are in series.

We can now determine the current coming out of the battery using Ohm’s Law.

Rearrange to solve for current.

The current coming out of the battery will be the same current that moves through the 4 Ohm resistor. So we can determine the voltage drop across the 4 ohm resistor.

We can then use Kirchoff’s loop law to determine the voltage drop from point to point .

Let’s analyze the loop that goes from the battery to the 4 ohm resistor and through the 3 ohm resistor.