Plane Geometry - GRE Quantitative Reasoning
Card 1 of 1504
Find the area of an equilateral triangle when one of its sides equals 4.
Find the area of an equilateral triangle when one of its sides equals 4.
Tap to reveal answer
All sides of an equilateral triangle are equal, so all sides of this triangle equal 4.
Area = 1/2 base * height, so we need to calculate the height: this is easy for an equilateral triangle, since you can bisect any such triangle into two identical 30:60:90 triangles.
The ratio of lengths of a 30:60:90 triangle is 1:√3:2. The side of the equilateral triangle is 4, and we divided the base in half when we bisected the triangle, so that give us a length of 2, so our triangle must have sides of 2, 4, and 2√3; thus we have our height.
One of our 30:60:90 triangles will have a base of 2 and a height of 2√3. Half the base is 1, so 1 * 2√3 = 2√3.
We have two of these triangles, since we divided the original triangle, so the total area is 2 * 2√3 = 4√3.
You can also solve for the area of any equilateral triangle by applying the formula (s2√3)/4, where s = the length of any side.
All sides of an equilateral triangle are equal, so all sides of this triangle equal 4.
Area = 1/2 base * height, so we need to calculate the height: this is easy for an equilateral triangle, since you can bisect any such triangle into two identical 30:60:90 triangles.
The ratio of lengths of a 30:60:90 triangle is 1:√3:2. The side of the equilateral triangle is 4, and we divided the base in half when we bisected the triangle, so that give us a length of 2, so our triangle must have sides of 2, 4, and 2√3; thus we have our height.
One of our 30:60:90 triangles will have a base of 2 and a height of 2√3. Half the base is 1, so 1 * 2√3 = 2√3.
We have two of these triangles, since we divided the original triangle, so the total area is 2 * 2√3 = 4√3.
You can also solve for the area of any equilateral triangle by applying the formula (s2√3)/4, where s = the length of any side.
← Didn't Know|Knew It →
What is the area of an equilateral triangle with a base of 
?
What is the area of an equilateral triangle with a base of
Tap to reveal answer
An equilateral triangle can be considered to be 2 identical 30-60-90 triangles, giving the triangle a height of 
. From there, use the formula for the area of a triangle:
An equilateral triangle can be considered to be 2 identical 30-60-90 triangles, giving the triangle a height of
← Didn't Know|Knew It →
An equilateral triangle is inscribed into a circle of radius 10. What is the area of the triangle?
An equilateral triangle is inscribed into a circle of radius 10. What is the area of the triangle?
Tap to reveal answer
To solve this equation, first note that a line drawn from the origin to a vertex of the equilateral triangle will bisect the angle of the vertex. Furthermore, the length of this line is equal to the radius:
That this creates in turn is a 30-60-90 right triangle. Recall that the ratio of the sides of a 30-60-90 triangle is given as:
Therefore, the length of the 
side can be found to be
This is also one half of the base of the triangle, so the base of the triangle can be found to be:
Furthermore, the length of the 
side is:
The vertical section rising from the origin is the length of the radius, which when combined with the shorter section above gives the height of the triangle:
The area of a triangle is given by one half the base times the height, so we can find the answer as follows:
To solve this equation, first note that a line drawn from the origin to a vertex of the equilateral triangle will bisect the angle of the vertex. Furthermore, the length of this line is equal to the radius:
That this creates in turn is a 30-60-90 right triangle. Recall that the ratio of the sides of a 30-60-90 triangle is given as:
Therefore, the length of the
This is also one half of the base of the triangle, so the base of the triangle can be found to be:
Furthermore, the length of the
The vertical section rising from the origin is the length of the radius, which when combined with the shorter section above gives the height of the triangle:
The area of a triangle is given by one half the base times the height, so we can find the answer as follows:
← Didn't Know|Knew It →
What is the length of a side of an equilateral triangle if the area is 
?
What is the length of a side of an equilateral triangle if the area is
Tap to reveal answer
The area of an equilateral triangle is 
.
So let's set-up an equation to solve for 
.
Cross multiply.
The 
cancels out and we get 
.
Then take square root on both sides and we get 
as the final answer.
The area of an equilateral triangle is
So let's set-up an equation to solve for
The
Then take square root on both sides and we get
← Didn't Know|Knew It →
If the area of an equilateral triangle is 
, what is the height of the triangle?
If the area of an equilateral triangle is
Tap to reveal answer
The area of an equilateral triangle is .
So let's set-up an equation to solve for .
Cross multiply.
The cancels out and we get 
.
Then take square root on both sides and we get 
. To find height, we need to realize by drawing a height we create 
triangles.
The height is opposite the angle 
. We can set-up a proportion. Side opposite 
is 
and the side of equilateral triangle which is opposite 
is 
.
Cross multiply.
Divide both sides by 
We can simplify this by factoring out a 
to get a final answer of 
.
The area of an equilateral triangle is
So let's set-up an equation to solve for
The
Then take square root on both sides and we get
The height is opposite the angle
We can simplify this by factoring out a
← Didn't Know|Knew It →
One side of an equilateral triangle is equal to 
Quantity A: The area of the triangle.
Quantity B: 
One side of an equilateral triangle is equal to
Quantity A: The area of the triangle.
Quantity B:
Tap to reveal answer
To find the area of an equilateral triangle, notice that it can be divided into two 
triangles:
The ratio of sides in a 
triangle is 
, and since the triangle is bisected such that the 
degree side is 
, the 
degree side, the height of the triangle, must have a length of 
.
The formula for the area of the triangle is given as:
So the area of an equilateral triangle can be written in term of the lengths of its sides as:
For this particular triangle, since 
, its area is equal to 
.
If the relation between ratios is hard to visualize, realize that 
To find the area of an equilateral triangle, notice that it can be divided into two
The ratio of sides in a
The formula for the area of the triangle is given as:
So the area of an equilateral triangle can be written in term of the lengths of its sides as:
For this particular triangle, since
If the relation between ratios is hard to visualize, realize that
← Didn't Know|Knew It →
Quantity A: The height of an equilateral triangle with an area of 
Quantity B: 
Which of the following is true?
Quantity A: The height of an equilateral triangle with an area of
Quantity B:
Which of the following is true?
Tap to reveal answer
This problem requires a bit of creative thinking (unless you have memorized the fact that an equilateral triangle always has an area equal to its side length times 
.
Consider the equilateral triangle:
Since this kind of triangle is a species of isoceles triangle, we know that we can drop down a height from the top vertex. This will create two equivalent triangles, one of which will look like:
This gives us a 30-60-90 triangle. We know that for such a triangle, the ratio of the side across from the 30-degree angle to the side across from the 60-degree angle is:
We can also say, given our figure, that the following equivalence must hold:
Solving for 
, we get:
Now, since 
, we know that 
must be smaller than 
. This means that 
or 
. Quantity B is larger than quantity A.
This problem requires a bit of creative thinking (unless you have memorized the fact that an equilateral triangle always has an area equal to its side length times
Consider the equilateral triangle:
Since this kind of triangle is a species of isoceles triangle, we know that we can drop down a height from the top vertex. This will create two equivalent triangles, one of which will look like:
This gives us a 30-60-90 triangle. We know that for such a triangle, the ratio of the side across from the 30-degree angle to the side across from the 60-degree angle is:
We can also say, given our figure, that the following equivalence must hold:
Solving for
Now, since
← Didn't Know|Knew It →
Quantity A: The height of an equilateral triangle with perimeter of 
.
Quantity B: 
Which of the following is true?
Quantity A: The height of an equilateral triangle with perimeter of
Quantity B:
Which of the following is true?
Tap to reveal answer
If the perimeter of our equilateral triangle is 
, each of its sides must be 
or 
. This gives us the following figure:
Since this kind of triangle is a species of isoceles triangle, we know that we can drop down a height from the top vertex. This will create two equivalent triangles, one of which will look like:
This gives us a 30-60-90 triangle. We know that for such a triangle, the ratio of the side across from the 30-degree angle to the side across from the 60-degree angle is:
Therefore, we can also say, given our figure, that the following equivalence must hold:
Solving for 
, we get:
Now, since 
, we know that 
must be smaller than 
. This means that 
or 
Therefore, quantity B is larger than quantity A.
If the perimeter of our equilateral triangle is
Since this kind of triangle is a species of isoceles triangle, we know that we can drop down a height from the top vertex. This will create two equivalent triangles, one of which will look like:
This gives us a 30-60-90 triangle. We know that for such a triangle, the ratio of the side across from the 30-degree angle to the side across from the 60-degree angle is:
Therefore, we can also say, given our figure, that the following equivalence must hold:
Solving for
Now, since
Therefore, quantity B is larger than quantity A.
← Didn't Know|Knew It →
Quantitative Comparison
Quantity A: The area of a triangle with a perimeter of 34
Quantity B: 30
Quantitative Comparison
Quantity A: The area of a triangle with a perimeter of 34
Quantity B: 30
Tap to reveal answer
A triangle with a fixed perimeter does not have to have a fixed area. For example, a triangle with sides 3, 4, and 5 has a perimeter of 12 and an area of 6. A triangle with sides 4, 4, and 4 also has a perimeter of 12 but not an area of 6. Thus the answer cannot be determined.
A triangle with a fixed perimeter does not have to have a fixed area. For example, a triangle with sides 3, 4, and 5 has a perimeter of 12 and an area of 6. A triangle with sides 4, 4, and 4 also has a perimeter of 12 but not an area of 6. Thus the answer cannot be determined.
← Didn't Know|Knew It →
If the height of the equilateral triangle is 
, then what is the length of a side of an equilateral triangle?
If the height of the equilateral triangle is
Tap to reveal answer
By having a height in an equilateral triangle, the angle is bisected therefore creating two 
triangles.
The height is opposite the angle . We can set-up a proportion.
Side opposite is and the side of equilateral triangle which is opposite is .
Cross multiply.
Divide both sides by 
Multiply top and bottom by 
to get rid of the radical.
By having a height in an equilateral triangle, the angle is bisected therefore creating two
The height is opposite the angle
Side opposite
← Didn't Know|Knew It →
Find the perimeter of an equilateral triangle with a height of 
.
Find the perimeter of an equilateral triangle with a height of
Tap to reveal answer
Perimeter is found by adding up all sides of the triangle. All sides in an equilateral triangle are equal, so we need to find the value of just one side to know the values of all sides.
The height of an equilateral triangle divides it into two equal 30:60:90 triangles, which will have side ratios of 1:2:√3. The height here is the √3 ratio, which in this case is equivalent to 8, so to get the length of the other two sides, we put 8 over √3 (8/√3) and 2 * 8/√3 = 16/√3, which is the hypotenuse of our 30:60:90 triangle.
The perimeter is then 3 * 16/√3, or 48/√3.
Perimeter is found by adding up all sides of the triangle. All sides in an equilateral triangle are equal, so we need to find the value of just one side to know the values of all sides.
The height of an equilateral triangle divides it into two equal 30:60:90 triangles, which will have side ratios of 1:2:√3. The height here is the √3 ratio, which in this case is equivalent to 8, so to get the length of the other two sides, we put 8 over √3 (8/√3) and 2 * 8/√3 = 16/√3, which is the hypotenuse of our 30:60:90 triangle.
The perimeter is then 3 * 16/√3, or 48/√3.
← Didn't Know|Knew It →
If the height of an equilateral triangle is 
, what is the perimeter?
If the height of an equilateral triangle is
Tap to reveal answer
By having a height in an equilateral triangle, the angle is bisected therefore creating two triangles.
The height is opposite the angle . We can set-up a proportion.
Side opposite is and the side of equilateral triangle which is opposite is .
Cross multiply.
Divide both sides by
Multiply top and bottom by to get rid of the radical.
Since each side is the same and there are three sides, we just multply the answer by three to get 
.
By having a height in an equilateral triangle, the angle is bisected therefore creating two
The height is opposite the angle
Side opposite
Since each side is the same and there are three sides, we just multply the answer by three to get
← Didn't Know|Knew It →
If area of equilateral triangle is 
, what is the perimeter?
If area of equilateral triangle is
Tap to reveal answer
The area of an equilateral triangle is .
So let's set-up an equation to solve for .
Cross multiply.
The cancels out and we get 
.
Then take square root on both sides and we get 
. Since we have three equal sides, we just multply 
by three to get 
as the final answer.
The area of an equilateral triangle is
So let's set-up an equation to solve for
The
Then take square root on both sides and we get
← Didn't Know|Knew It →
A triangle has three internal angles of 75, 60, and x. What is x?
A triangle has three internal angles of 75, 60, and x. What is x?
Tap to reveal answer
The internal angles of a triangle must add up to 180. 180 - 75 -60= 45.
The internal angles of a triangle must add up to 180. 180 - 75 -60= 45.
← Didn't Know|Knew It →
The radius of the circle is 2. What is the area of the shaded equilateral triangle?
The radius of the circle is 2. What is the area of the shaded equilateral triangle?
Tap to reveal answer
This is easier to see when the triangle is divided into six parts (blue). Each one contains an angle which is half of 120 degrees and contains a 90 degree angle. This means each triangle is a 30/60/90 triangle with its long side equal to the radius of the circle. Knowing that means that the height of each triangle is 
and the base is 
.
Applying 
and multiplying by 6 gives 
).
This is easier to see when the triangle is divided into six parts (blue). Each one contains an angle which is half of 120 degrees and contains a 90 degree angle. This means each triangle is a 30/60/90 triangle with its long side equal to the radius of the circle. Knowing that means that the height of each triangle is
Applying
← Didn't Know|Knew It →
An equilateral triangle has a side length of 4. What is its height?
An equilateral triangle has a side length of 4. What is its height?
Tap to reveal answer
If an equilateral triangle is divided in 2, it forms two 30-60-90 triangles. Therefore, the side of the equilateral triangle is the same as the hypotenuse of a 30-60-90 triangle. The side lengths of a 30-60-90 triangle adhere to the ratio x: x√3 :2x. since we know the hypothesis is 4, we also know that the base is 2 and the height is 2√3.
If an equilateral triangle is divided in 2, it forms two 30-60-90 triangles. Therefore, the side of the equilateral triangle is the same as the hypotenuse of a 30-60-90 triangle. The side lengths of a 30-60-90 triangle adhere to the ratio x: x√3 :2x. since we know the hypothesis is 4, we also know that the base is 2 and the height is 2√3.
← Didn't Know|Knew It →
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
Tap to reveal answer
cannot be the side lengths of a right triangle. 
does not equal 
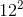. Also, special right triangle 
and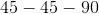 
rules can eliminate all the other choices.
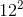
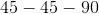
← Didn't Know|Knew It →
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
Daria and Ashley start at the same spot and walk their two dogs to the park, taking different routes. Daria walks 1 mile north and then 1 mile east. Ashley walks her dog on a path going northeast that leads directly to the park. How much further does Daria walk than Ashley?
Tap to reveal answer
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
First let's calculate how far Daria walks. This is simply 1 mile north + 1 mile east = 2 miles. Now let's calculate how far Ashley walks. We can think of this problem using a right triangle. The two legs of the triangle are the 1 mile north and 1 mile east, and Ashley's distance is the diagonal. Using the Pythagorean Theorem we calculate the diagonal as √(12 + 12) = √2. So Daria walked 2 miles, and Ashley walked √2 miles. Therefore the difference is simply 2 – √2 miles.
← Didn't Know|Knew It →
Which of the following sets of sides cannnot belong to a right triangle?
Which of the following sets of sides cannnot belong to a right triangle?
Tap to reveal answer
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
To answer this question without plugging all five answer choices in to the Pythagorean Theorem (which takes too long on the GRE), we can use special triangle formulas. Remember that 45-45-90 triangles have lengths of x, x, x√2. Similarly, 30-60-90 triangles have lengths x, x√3, 2x. We should also recall that 3,4,5 and 5,12,13 are special right triangles. Therefore the set of sides that doesn't fit any of these rules is 6, 7, 8.
← Didn't Know|Knew It →
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
Max starts at Point A and travels 6 miles north to Point B and then 4 miles east to Point C. What is the shortest distance from Point A to Point C?
Tap to reveal answer
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
This can be solved with the Pythagorean Theorem.
62 + 42 = _c_2
52 = _c_2
c = √52 = 2√13
← Didn't Know|Knew It →