Other Quadrilaterals - GMAT Quantitative

Card 1 of 456

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

Note: Figure NOT drawn to scale

What is the area of Quadrilateral , above?

Tap to reveal answer

Answer

Quadrilateral is a composite of two right triangles, $\Delta ADU$ and $\Delta DUQ$ , so we find the area of each and add the areas. First, we need to find and , since the area of a right triangle is half the product of the lengths of its legs.

By the Pythagorean Theorem:

$\left (AD \right )^{2} +\left ( AU\right ) ^{2} =\left ( DU\right ) ^{2}$

$\left (AD \right )^{2} +4 ^{2} =5 ^{2}$

$\left (AD \right )^{2} +16 =25$

$\left (AD \right )^{2} +16 -16 =25 -16$

$\left (AD \right )^{2} =9$

Also by the Pythagorean Theorem:

$\left ( QU\right ) ^{2} + \left ( DU\right ) ^{2}=\left ( DQ\right ) ^{2}$

$\left ( QU\right ) ^{2} + 5^{2}=13^{2}$

$\left ( QU\right ) ^{2} + 25 =169$

$\left ( QU\right ) ^{2} + 25 -25=169 -25$

$\left ( QU\right ) ^{2} =144$

The area of $\Delta ADU$ is $\frac{1}{2} \cdot AD \cdot AU = \frac{1}{2} \cdot 3 \cdot 4 = 6$ .

The area of $\Delta DUQ$ is $\frac{1}{2} \cdot DU \cdot QU = \frac{1}{2} \cdot 5 \cdot 12 = 30$ .

Add the areas to get , the area of Quadrilateral .

← Didn't Know|Knew It →

Question

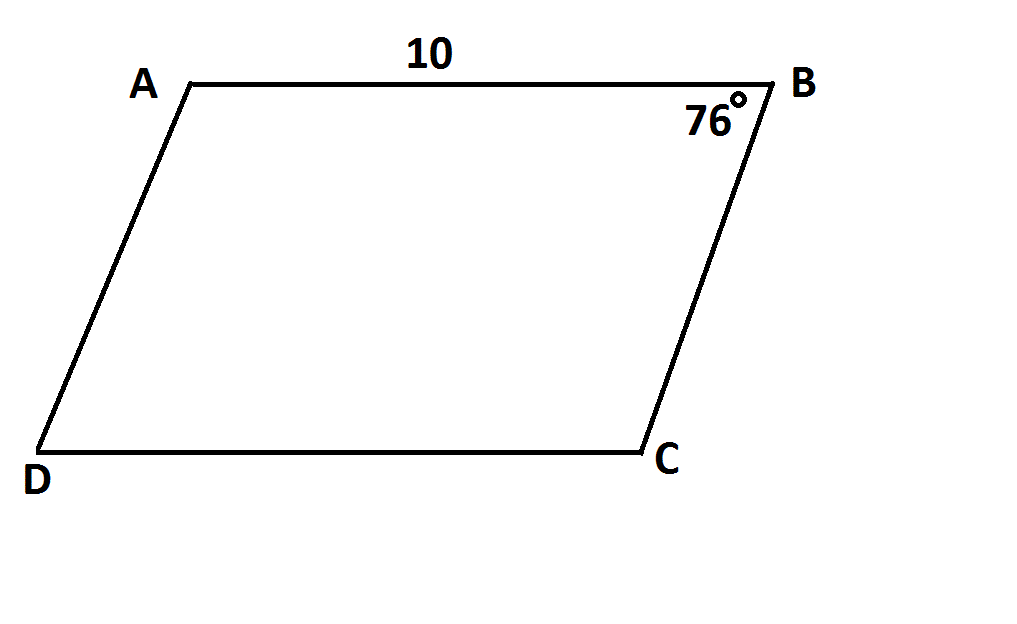
Note: Diagram is NOT drawn to scale.

Refer to the above diagram.

Any of the following facts alone would be enough to prove that $\textrm{Quad} ; ABCD$ is not a parallelogram, EXCEPT:

Tap to reveal answer

Answer

Opposite sides of a parallelogram are congruent; if , then $CD \neq AB$ , violating this condition.

Consecutive angles of a parallelogram are supplementary; if $m \angle A = 114^{\circ}$ , then $m \angle A + m \angle B= 114 + 76 = 190$ , violating this condition.

Opposite angles of a parallelogram are congruent; if $m \angle D <76^{\circ}$ , then $m \angle D \neq m \angle B$ , violating this condition.

Adjacent sides of a parallelogram, however, may or may not be congruent, so the condition that would not by itself prove that the quadrilateral is not a parallelogram.

← Didn't Know|Knew It →

Question

Which of the following can not be the measures of the four interior angles of a quadrilateral?

Tap to reveal answer

Answer

The four interior angles of a quadrilateral measure a total of $360^{\circ }$ , so we test each group of numbers to see if they have this sum.

This last group does not have the correct sum, so it is the correct choice.

← Didn't Know|Knew It →

Question

A circle can be circumscribed about each of the following figures except:

Tap to reveal answer

Answer

A circle can be circumscribed about any triangle regardless of its sidelengths or angle measures, so we can eliminate the two triangle choices.

A circle can be circumscribed about a quadrilateral if and only if both pairs of its opposite angles are supplementary. An isosceles trapezoid has this characteristic; this can be proved by the fact that base angles are congruent, and by the Same-Side Interior Angles Statement. For a parallelogram to have this characteristic, since opposite angles are congruent also, all angles must measure $90^{\circ }$ ; the rectangle fits this description, but the rhombus does not.

← Didn't Know|Knew It →

Question

Two angles of a parallelogram measure $\left ( x + 70 \right )^{\circ }$ and $\left ( 2x\right +5) ^{\circ }$ . What are the possible values of ?

Tap to reveal answer

Answer

Case 1: The two angles are opposite angles of the parallelogram. In this case, they are congruent, and

Case 2: The two angles are consecutive angles of the parallelogram. In this case, they are supplementary, and

$\left ( 2x +5 \right )+\left ( x + 70 \right ) = 180$

$3x \div 3 = 105\div 3$

← Didn't Know|Knew It →

Question

Rhombus has two diagonals that intersect at point ; $\angle RHO = 80 ^{\circ }$ .

What is $m \angle RPH$ ?

Tap to reveal answer

Answer

The diagonals of a rhombus always intersect at right angles, so $m \angle HPO = 90 ^{\circ }$ . The measures of the interior angles of the rhombus are irrelevant.

← Didn't Know|Knew It →

Question

Quadrilateral is inscribed in circle $\bigodot$ . $m \angle A = 100 ^{\circ }$ . What is $m \angle Q$ ?

Tap to reveal answer

Answer

Two opposite angles of a quadrilateral inscribed inside a circle are supplementary, so

$m \angle Q = 180^{\circ } - m \angle A = 180^{\circ } - 100^{\circ } = 80^{\circ }$

← Didn't Know|Knew It →

Question

Note: Figure NOT drawn to scale.

The above figure is of a rhombus and one of its diagonals. What is equal to?

Tap to reveal answer

Answer

The four sides of a rhombus are congruent, so a diagonal of the rhombus cuts it into two isosceles triangles. The two angles adjacent to the diagonal are congruent, so the third angle, the one marked, measures:

$\left (180 - 2 \times 24 \right )^{\circ } = \left (180 -48 \right )^{\circ } = 132^{\circ }$

← Didn't Know|Knew It →

Question

Refer to the above figure. You are given that Polygon is a parallelogram, but NOT that it is a rectangle.

Which of the following statements is not enough to prove that Polygon is also a rectangle?

Tap to reveal answer

Answer

To prove that Polygon is also a rectangle, we need to prove that any one of its angles is a right angle.

If $\overline{BC} \perp \overline{DC}$ , then by definition of perpendicular lines, $\angle BCD$ is right.

If $m \angle 1 = 90^{\circ }$ , then, since $\angle 1$ and $\angle BCD$ form a linear pair, $\angle BCD$ is right.

If $(AD)^{2} + (DC)^{2} = (AC)^{2}$ , then, by the Converse of the Pythagorean Theorem, $\Delta ADC$ is a right triangle with right angle $\angle D$ .

If $\angle BAC$ and $\angle CAD$ are complementary angles, then, since $m \angle BAC + m \angle CAD =m \angle BA D$

$m \angle BAD = m \angle BAC + m \angle CAD = 90 ^{\circ }$ , making $m \angle BAD$ right.

However, since, by definition of a parallelogram, $\overline{AB } \parallel \overline{ CD }$ , by the Alternate Interior Angles Theorem, $\angle BAC \cong \angle ACD$ regardless of whether the parallelogram is a rectangle or not.

← Didn't Know|Knew It →

Question

What is the area of a trapezoid with a height of 7, a base of 5, and another base of 13?

Tap to reveal answer

Answer

$area = \frac{(b_{1}+ b_{2}\cdot h)}{2} = \frac{(5 + 13)\cdot 7}{2} = \frac{18\cdot 7}{2} = \frac{126}{2} = 63$

← Didn't Know|Knew It →

Question

A circle can be circumscribed about each of the following figures except:

Tap to reveal answer

Answer

A circle can be circumscribed about any triangle regardless of its sidelengths or angle measures, so we can eliminate the two triangle choices.

A circle can be circumscribed about any regular polygon, so we can eliminate those two choices as well.

The correct choice is that each figure can have a circle circumscribed about it.

← Didn't Know|Knew It →

Question

What is the area of a quadrilateral on the coordinate plane with vertices ?

Tap to reveal answer

Answer

As can be seen from this diagram, this is a parallelogram with base 8 and height 4:

The area of this parallelogram is the product of its base and its height:

$A = bh = 8 \cdot 4 = 32$

← Didn't Know|Knew It →

Question

What is the area of a quadrilateral on the coordinate plane with vertices ?

Tap to reveal answer

Answer

As can be seen in this diagram, this is a trapezoid with bases 10 and 5 and height 8.

Setting in the following formula, we can calculate the area of the trapezoid:

$A = \frac{1}{2} (B + b) h = \frac{1}{2} \cdot (10 + 5)\cdot 8 = 60$

← Didn't Know|Knew It →

Question

What is the area of the quadrilateral on the coordinate plane with vertices ?

Tap to reveal answer

Answer

The quadrilateral formed is a trapezoid with two horizontal bases. One base connects (0,0) and (9,0) and therefore has length ; the other connects (4,7) and (7,7) and has length . The height is the vertical distance between the two bases, which is the difference of the coorindates: . Therefore, the area of the trapezoid is

$A = \frac{1}{2} (B + b ) h = \frac{1}{2} \cdot (9+3 ) \cdot 7 = 42$

← Didn't Know|Knew It →

Question

What is the area of the quadrilateral on the coordinate plane with vertices .

Tap to reveal answer

Answer

The quadrilateral is a trapezoid with horizontal bases; one connects and and has length , and the other connects and and has length . The height is the vertical distance between the bases, which is the difference of the -coordinates; this is . Substitute in the formula for the area of a trapezoid:

$A = \frac{1}{2} (B + b)h = \frac{1}{2}\cdot (10+6) \cdot 6 = 48$

← Didn't Know|Knew It →

Question

What is the area of the quadrilateral on the coordinate plane with vertices ?

Tap to reveal answer

Answer

The quadrilateral is a parallelogram with two vertical bases, each with length . Its height is the distance between the bases, which is the difference of the -coordinates: . The area of the parallelogram is the product of its base and its height:

$7 \times 5 = 35$

← Didn't Know|Knew It →

Question

Give the area of the above parallelogram if .

Tap to reveal answer

Answer

Multiply height by base to get the area.

By the 30-60-90 Theorem:

$CD= \frac{BC}{2} = \frac{10}{2}} = 5$ .

$BD =CD \sqrt{3} = 5\sqrt{3}$

The area is therefore

$BD \cdot CD = 5\sqrt{3} \cdot 5= 25\sqrt{3}$

← Didn't Know|Knew It →

Question

Give the area of the above parallelogram if .

Tap to reveal answer

Answer

Multiply height by base to get the area.

By the 45-45-90 Theorem,

$BD=CD = BC \div \sqrt{2} = \frac{16}{\sqrt{2}} = \frac{16\cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{16 \sqrt{2}}{2} = 8 \sqrt{2}$ .

Since the product of the height and the base of a parallelogram is its area,

$A = BD \cdot CD$

$= 8 \sqrt{2} \cdot 8 \sqrt{2}$

$= 8\cdot 8 \cdot \sqrt{2} \cdot \sqrt{2}$

$= 8\cdot 8 \cdot 2$

← Didn't Know|Knew It →

Question

Give the area of the above parallelogram if .

Tap to reveal answer

Answer

Multiply height by base to get the area.

By the 30-60-90 Theorem:

$BD= \frac{BC}{2} = \frac{30}{2}} = 15$ .

$CD =BD \sqrt{3} = 15\sqrt{3}$

The area is therefore

$BD \cdot CD =15 \cdot 15\sqrt{3} = 225\sqrt{3}$

← Didn't Know|Knew It →

Question

The above figure shows a rhombus . Give its area.

Tap to reveal answer

Answer

Construct the other diagonal of the rhombus, which, along with the first one, form a pair of mutual perpendicular bisectors.

By the Pythagorean Theorem,

$n = \sqrt{12^{2}- 10^{2}} =\sqrt{144- 100} = \sqrt{44}= \sqrt{4}\cdot \sqrt{11} = 2 \sqrt{11}$

The rhombus can be seen as the composite of four congruent right triangles, each with legs 10 and $2 \sqrt{11}$ , so the area of the rhombus is

$A = 4 \cdot \frac{1}{2}\cdot 10 \cdot 2\sqrt{11} =40 \sqrt{11}$ .

← Didn't Know|Knew It →

0

Knew It