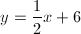How to find the equation of a parallel line

Geometry · Learn by Concept

Help Questions

Geometry › How to find the equation of a parallel line

1 - 8

A line is parallel to the line of the equation

and passes through the point .

Give the equation of the line in standard form.

CORRECT

None of the other choices gives the correct response.

Explanation

Two parallel lines have the same slope. Therefore, it is necessary to find the slope of the line of the equation

Rewrite the equation in slope-intercept form . , the coefficient of , will be the slope of the line.

Add to both sides:

Multiply both sides by $\frac{1}{7}$ , distributing on the right:

$\frac{1}{7} \cdot 7y = \frac{1}{7} \cdot( -5x+32)$

$y = -\frac{5}{7}x+\frac{32}{7}$

The slope of this line is $-\frac{5}{7}$ . The slope of the first line will be the same. The slope-intercept form of the equation of this line will be

$y =-\frac{5}{7}x+b$ .

To find , set and and solve:

$8 =-\frac{5}{7} (-2)+b$

$8 = \frac{10}{7} +b$

$\frac{56}{7} = \frac{10}{7} +b$

Subtract $\frac{10}{7}$ from both sides:

$\frac{56}{7} - \frac{10}{7} = \frac{10}{7} +b - \frac{10}{7}$

$b = \frac{46}{7}$

The slope-intercept form of the equation is $y =-\frac{5}{7}x+ \frac{46}{7}$

To rewrite in standard form with integer coefficients:

Multiply both sides by 7:

$7 y =7\left (-\frac{5}{7}x+ \frac{46}{7} \right )$

$7 y =7\left (-\frac{5}{7}x \right ) +7\left ( \frac{46}{7} \right )$

Add to both sides:

the correct equation in standard form.

Which one of these equations is parallel to:

CORRECT

$y=\frac{1}{3}x$

$y=\frac{-1}{3}+4$

Explanation

Equations that are parallel have the same slope.

For the equation:

The slope is since that is how much changes with increment of .

The only other equation with a slope of is:

Suppose a line . What is the equation of a parallel line that intersects point ?

CORRECT

Explanation

A line parallel to must have a slope of two. Given the point and the slope, use the slope-intercept formula to determine the -intercept by plugging in the values of the point and solving for :

Plug the slope and the -intercept into the slope-intercept formula:

Find the equation of the line parallel to that passes through the point .

CORRECT

Explanation

Write in slope intercept form, , to determine the slope, :

$y=-x+\frac{1}{3}$

The slope is:

Given the slope, use the point and the equation to solve for the value of the -intercept, . Substitute the known values.

With the known slope and the -intercept, plug both values back to the slope intercept formula. The answer is .

Given , find the equation of a line parallel.

CORRECT

$y=\frac{1}{3}x-20$

$y=\frac{-1}{3}-20$

Explanation

The definition of a parallel line is that the lines have the same slopes, but different intercepts. The only answer with the same slope is .

What equation is parallel to:

CORRECT

Explanation

To find a parallel line to

we need to find another equation with the same slope of or .

The only equation that satisfies this is .

What equation is parallel to:

CORRECT

$y=\frac{1}{5}x+4$

$y=\frac{-1}{5}x+5$

Explanation

To find an equation that is parallel to

we need to find an equation with the same slope of .

Basically we are looking for another equation with .

The only other equation that satisfies this is

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point ?

$\small y=\frac{1}{2}x$

CORRECT

$\small y=-2x+10$

$\small y=\frac{1}{2}x+6$

$\small y=2x-6$

Explanation

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.