Quadrilaterals - Geometry

Card 1 of 600

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

Find the area of the rhombus shown below. You will have to find the lengths of the sides as well.

The rhombus shown has the following coordinates:

Round to the nearest hundredth.

Tap to reveal answer

Answer

Finding the area of a rhombus follows the formula:

$\frac{p\times q}{2}$

In this rhombus, you will find that , which are the two x coordinates.

The length of q is a more involved process. You can find q by using the Pythagorean Theorem.

$\sqrt{65}=8.06$ .

Therefore, the area is

$\frac{6\times 8.06}{2}=24.18$ .

← Didn't Know|Knew It →

Question

Find the area of the rhombus below.

Tap to reveal answer

Answer

Recall that the diagonals of the rhombus are perpendicular bisectors. From the given side and the given diagonal, we can find the length of the second diagonal by using the Pythagorean Theorem.

$\text{side}^2=(\frac{\text{diagonal 1}}{2})^2-(\frac{\text{diagonal 2}}{2})^2$

Let the given diagonal be diagonal 1, and rearrange the equation to solve for diagonal 2.

$(\frac{\text{diagonal 2}}{2})^2=\text{side}^2-(\frac{\text{diagonal 1}}{2})^2$

$(\frac{\text{diagonal 2}}{2})=\sqrt{\text{side}^2-(\frac{\text{diagonal 1}}{2})^2}$

$\text{diagonal 2}=2\sqrt{\text{side}^2-(\frac{\text{diagonal 1}}{2})^2}$

Plug in the given side and diagonal to find the length of diagonal 2.

$\text{diagonal 2}=2\sqrt{13^2-(\frac{10}{2})^2}=2\sqrt{144}=24$

Now, recall how to find the area of a rhombus:

$\text{Area of Rhombus}=\frac{(\text{diagonal 1})(\text{diagonal 2})}{2}$

Plug in the two diagonals to find the area.

$\text{Area of Rhombus}=\frac{(10)(24)}{2}=120$

← Didn't Know|Knew It →

Question

Find the area of the rhombus below.

Tap to reveal answer

Answer

Recall that the diagonals of the rhombus are perpendicular bisectors. From the given side and the given diagonal, we can find the length of the second diagonal by using the Pythagorean Theorem.

$\text{side}^2=(\frac{\text{diagonal 1}}{2})^2-(\frac{\text{diagonal 2}}{2})^2$

Let the given diagonal be diagonal 1, and rearrange the equation to solve for diagonal 2.

$(\frac{\text{diagonal 2}}{2})^2=\text{side}^2-(\frac{\text{diagonal 1}}{2})^2$

$(\frac{\text{diagonal 2}}{2})=\sqrt{\text{side}^2-(\frac{\text{diagonal 1}}{2})^2}$

$\text{diagonal 2}=2\sqrt{\text{side}^2-(\frac{\text{diagonal 1}}{2})^2}$

Plug in the given side and diagonal to find the length of diagonal 2.

$\text{diagonal 2}=2\sqrt{15^2-(\frac{16}{2})^2}=2\sqrt{161}$

Now, recall how to find the area of a rhombus:

$\text{Area of Rhombus}=\frac{(\text{diagonal 1})(\text{diagonal 2})}{2}$

Plug in the two diagonals to find the area.

$\text{Area of Rhombus}=\frac{(16)(2\sqrt{161})}{2}=203.02$

Make sure to round to places after the decimal.

← Didn't Know|Knew It →

Question

What is the area of the following kite?

Tap to reveal answer

Answer

The formula for the area of a kite:

$A = \frac{1}{2} (a)(b)$ ,

where represents the length of one diagonal and represents the length of the other diagonal.

Plugging in our values, we get:

$A = \frac{1}{2} (4: m)(5: m)$

$A = \frac{1}{2} (20: m^2) = 10: m^2$

← Didn't Know|Knew It →

Question

Which of the following shapes is a kite?

Tap to reveal answer

Answer

A kite is a four-sided shape with straight sides that has two pairs of sides. Each pair of adjacent sides are equal in length. A square is also considered a kite.

← Didn't Know|Knew It →

Question

Two congruent equilateral triangles with sides of length are connected so that they share a side. Each triangle has a height of . Express the area of the shape in terms of .

Tap to reveal answer

Answer

The shape being described is a rhombus with side lengths 1. Since they are equilateral triangles connected by one side, that side becomes the lesser diagonal, so .

The greater diagonal is twice the height of the equaliteral triangles, .

The area of a rhombus is half the product of the diagonals, so:

$A=\frac{pq}{2}=\frac{1 \cdot 2h}{2}=h$

← Didn't Know|Knew It →

Question

The diagonal lengths of a kite are and . What is the area?

Tap to reveal answer

Answer

The area of a kite is given below. Substitute the given diagonals to find the area.

$A= \frac{d1\cdot d2}{2} = \frac{6\cdot 7}{2}=21$

← Didn't Know|Knew It →

Question

Find the area of a kite if the length of the diagonals are and .

Tap to reveal answer

Answer

Substitute the given diagonals into the area formula for kites. Solve and simplify.

$A=\frac{d1\cdot d2}{2} = \frac{3\cdot 10}{2}=15$

← Didn't Know|Knew It →

Question

Find the area of a kite if the diagonal dimensions are and .

Tap to reveal answer

Answer

The area of the kite is given below. The FOIL method will need to be used to simplify the binomial.

$A=\frac{d1\cdot d2}{2}=\frac{(x+3)(x-6)}{2}= \frac{x^2-6x+3x-18}{2}$

$A= \frac{x^2-3x-18}{2}$

← Didn't Know|Knew It →

Question

Find the area of a kite if one diagonal is long, and the other diagonal is long.

Tap to reveal answer

Answer

The formula for the area of a kite is

$A=\frac{d_1\cdot d_2}{2}$

Plug in the values for each of the diagonals and solve.

$A = \frac{2\cdot 10}{2}=\frac{20}{2}=10:cm^2$

← Didn't Know|Knew It →

Question

The diagonals of a kite are $\sqrt10:cm$ and $\sqrt5:cm$ . Find the area.

Tap to reveal answer

Answer

The formula for the area for a kite is

$A=\frac{d_1\cdot d_2}{2}$ , where and are the lengths of the kite's two diagonals. We are given the length of these diagonals in the problem, so we can substitute them into the formula and solve for the area:

$A = \frac{d1\cdot d2}{2} = \frac{\sqrt10 \cdot \sqrt5}{2} = \frac{\sqrt50}{2} = \frac{5\sqrt2}{2}:cm^2$

← Didn't Know|Knew It →

Question

The diagonals of a kite are and $\frac{1}{x}:units$ . Express the kite's area in simplified form.

Tap to reveal answer

Answer

Write the formula for the area of a kite.

$A=\frac{d_1\cdot d_2}{2}$

Substitute the diagonals and reduce.

$A=\frac{d_1\cdot d_2}{2} = \frac{(2x+1)(\frac{1}{x})}{2}$

Multiply the parenthetical elements together by distributing the $\frac{1}{x}$ :

$A= \frac{(2x\cdot \frac{1}{x})+(1\cdot \frac{1}{x})}{2}$

$A=\frac{\frac{2x}{x}+\frac{1}{x}}{2}$

$A=\frac{2+\frac{1}{x}}{2}$

You can consider the outermost fraction with in the denominator as multiplying everything in the numerator by $\frac{1}{2}$ :

$A=(\frac{1}{2})(2+\frac{1}{x})$

$A=1+\frac{1}{2x}$

Change the added to $\frac{2x}{2x}$ to create a common denominator and add the fractions to arrive at the correct answer:

$A=\frac{2x}{2x} + \frac{1}{2x} = \frac{2x+1}{2x}$

← Didn't Know|Knew It →

Question

If the diagonals of a kite are $\frac{1}{6x}:units$ and , express the area in simplified form.

Tap to reveal answer

Answer

Write the formula for the area of a kite:

$A=\frac{d_1 \cdot d_2}{2}$

Substitute the given diagonals:

$A = \frac{(\frac{1}{6x})(2x+5)}{2}$

Distribute the $\frac{1}{6x}$ :

$A= \frac{\frac{1}{3}+\frac{5}{6x}}{2}$

Create a common denominator for the two fractions in the numerator:

$A= \frac{\frac{2x}{6x}+\frac{5}{6x}}{2}$

$A= \frac{\frac{2x+5}{6x}}{2}$

You can consider the outermost division by as multiplying everything in the numerator by $\frac{1}{2}$ :

$A=(\frac{1}{2})(\frac{2x+5}{6x})$

Multiply across to arrive at the correct answer:

$A=\frac{2x+5}{12x}$

← Didn't Know|Knew It →

Question

Find the area of a kite with the diagonal lengths of and .

Tap to reveal answer

Answer

Write the formula to find the area of a kite. Substitute the diagonals and solve.

$A=\frac{d1 \cdot d2}{2} = \frac{2a \cdot 2b}{2} =2ab$

← Didn't Know|Knew It →

Question

Find the area of a kite with diagonal lengths of and .

Tap to reveal answer

Answer

Write the formula for the area of a kite.

$A= \frac{d1\cdot d2}{2}$

Plug in the given diagonals.

$A= \frac{(a+b)\cdot (2a-2b)}{2}$

Pull out a common factor of two in and simplify.

$A= \frac{(a+b)\cdot2(a-b)}{2}$

Use the FOIL method to simplify.

← Didn't Know|Knew It →

Question

Show algebraically how the formula of the area of a kite is developed.

Tap to reveal answer

Answer

The given kite is divded into two congruent triangles.

Each triangle has a height $h = \frac{1}{2}d_{1}$ and a base $b = d_{2}$ .

The area of each triangle is $A = \frac{1}{2}bh$ .

The areas of the two triangles are added together,

$= \frac{1}{2}(\frac{1}{2}d_{1})(d_{2}) + \frac{1}{2}(\frac{1}{2}d_{1})(d_{2})$

$= \frac{1}{4}d_{1}d_{2} +\frac{1}{4}d_{1}d_{2}$

$=\frac{1}{2}d_{1}d_{2}$

← Didn't Know|Knew It →

Question

Find the area of a kite, if the diagonals of the kite are $\sqrt{8}, \sqrt{7}$ .

Tap to reveal answer

Answer

You find the area of a kite by using the lengths of the diagonals.

$A=\frac{d_{1}\times d_{2}}{2}$

$A=\frac{\sqrt{8}\times \sqrt{7}}{2}$ , which is equal to $\frac{\sqrt{56}}{2}$ .

You can reduce this to,

$\frac{\sqrt{2\cdot 4\cdot 7}}{2}=\frac{2\sqrt{2\cdot 7}}{2}=\sqrt{2\cdot 7}=\sqrt{14}$ for the final answer.

← Didn't Know|Knew It →

Question

The rectangle area $A_{R}$ is 220. What is the area $A_{K}$ of the inscribed

kite ?

Tap to reveal answer

Answer

The measures of the kite diagonals $\overline{GH}$ and $\overline{BE}$ have to be found.

Using the circumscribed rectangle, , and .

has to be found to find $m(\overline{GH})$ .

The rectangle area $A_{R} = 220$ .

$A_{R} = bh$ .

From step 1) and step 2), using substitution, .

Solving the equation for x,

$\frac{(19 + x)(10)}{10} = \frac{220}{10}$

$m(\overline{GH}) = 19 + 3 = 22$

Kite area $A_{K} = \frac{1}{2} \cdot 22 \cdot 10 = 110$

← Didn't Know|Knew It →

Question

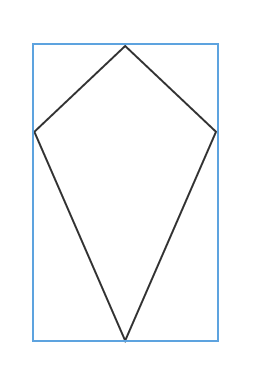
The area of the rectangle is , what is the area of the kite?

Tap to reveal answer

Answer

The area of a kite is half the product of the diagonals.

$A=\frac{p \cdot q}{2}$

The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.

Therefore our equation becomes:

$A=\frac{l \cdot w}{2}$ .

We also know the area of the rectangle is $A=l \cdot w=80$ . Substituting this value in we get the following:

$A=\frac{l \cdot w}{2}=\frac{80}{2}=40$

Thus,, the area of the kite is .

← Didn't Know|Knew It →

Question

Given: Quadrilateral such that $\overline{KI} \cong \overline{KE}$ , $\overline{TI} \cong \overline{TE}$ , $m \angle K = 60^{\circ }$ , $\angle T$ is a right angle, and diagonal $\overline{I E}$ has length 24.

Give the length of diagonal $\overline{KT}$ .

Tap to reveal answer

Answer

The Quadrilateral is shown below with its diagonals $\overline{I E}$ and $\overline{KT}$ .

. We call the point of intersection :

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, $\overline{KT}$ bisects the $60 ^{\circ }$ and $90^{\circ }$ angles of the kite. Consequently, $\bigtriangleup KXI$ is a 30-60-90 triangle and $\bigtriangleup TXI$ is a 45-45-90 triangle. Also, the diagonal that connects the common vertices of the pairs of adjacent sides bisects the other diagonal, making the midpoint of $\overline{IE}$ . Therefore,

$IX = \frac{1}{2} \cdot IE = \frac{1}{2} \cdot 24 = 12$ .

By the 30-60-90 Theorem, since $\overline{IX}$ and $\overline{KX}$ are the short and long legs of $\bigtriangleup KXI$ ,

$KX = IX \cdot \sqrt{3}= 12 \sqrt{3}$

By the 45-45-90 Theorem, since $\overline{IX}$ and $\overline{XT}$ are the legs of a 45-45-90 Theorem,

.

The diagonal $\overline{KT}$ has length

$KT =XT + KX= 12+ 12\sqrt{3}$ .

← Didn't Know|Knew It →

0

Knew It