Squares, Rectangles, and Parallelograms - GED Math
Card 0 of 505

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is six feet wide throughout. Which of the following polynomials gives the perimeter of the garden, in feet?

Note: Figure NOT drawn to scale
Refer to the above figure, which shows a rectangular garden (in green) surrounded by a dirt path (in brown). The dirt path is six feet wide throughout. Which of the following polynomials gives the perimeter of the garden, in feet?
The length of the garden, in feet, is  feet less than that of the entire lot, or
feet less than that of the entire lot, or
 .
.
The width of the garden, in feet, is  less than that of the entire lot, or
less than that of the entire lot, or
 .
.
The perimeter, in feet, is twice the sum of the two:


The length of the garden, in feet, is 

The width of the garden, in feet, is 

The perimeter, in feet, is twice the sum of the two:
Compare your answer with the correct one above
Your mother made a casserole in a pan whose length is 9 inches and whose width is one and a half times the length. What is the area of the casserole pan?
Your mother made a casserole in a pan whose length is 9 inches and whose width is one and a half times the length. What is the area of the casserole pan?
To find the area, you need to multiply the dimensions. First, however, we need to find our width.
We can find our width by using the clue: "...one and a half times the length"
So, do the following:

Next, perform the following operation:

Making our answer:

To find the area, you need to multiply the dimensions. First, however, we need to find our width.
We can find our width by using the clue: "...one and a half times the length"
So, do the following:
Next, perform the following operation:
Making our answer:
Compare your answer with the correct one above
Find the area of a square if the side length is  .
.
Find the area of a square if the side length is 
The area of a square is: 
Substitute the side into the area formula of the square.

Squaring a radical will leave just the term inside the radical.
The area is: 
The area of a square is:
Substitute the side into the area formula of the square.
Squaring a radical will leave just the term inside the radical.
The area is:
Compare your answer with the correct one above
A rectangle has a diagonal of  and a length of
and a length of  . What is the area of the rectangle?
. What is the area of the rectangle?
A rectangle has a diagonal of 

The rectangle given in the question can be drawn out as thus:

Notice that the diagonal is also the hypotenuse of a right triangle that has the length and width of the rectangle as its legs. Thus, use the Pythagorean Theorem to find the length of the width of the rectangle.




Next, recall how to find the area of a rectangle.

Plug in the length and width of the rectangle.

The rectangle given in the question can be drawn out as thus:

Notice that the diagonal is also the hypotenuse of a right triangle that has the length and width of the rectangle as its legs. Thus, use the Pythagorean Theorem to find the length of the width of the rectangle.
Next, recall how to find the area of a rectangle.
Plug in the length and width of the rectangle.
Compare your answer with the correct one above
Suppose you receive a square sheet of wood which you are planning on making into a box. If the sheet is  , find the perimeter of the sheet.
, find the perimeter of the sheet.
Suppose you receive a square sheet of wood which you are planning on making into a box. If the sheet is 
Suppose you receive a square sheet of wood which you are planning on making into a box. If the sheet is  , find the perimeter of the sheet.
, find the perimeter of the sheet.
To find the perimeter of a rectangle, use the following formula:

So, let's plug in our length and width and solve:

Suppose you receive a square sheet of wood which you are planning on making into a box. If the sheet is 
To find the perimeter of a rectangle, use the following formula:
So, let's plug in our length and width and solve:
Compare your answer with the correct one above
Use the following rectangle to answer the question:

Find the perimeter.
Use the following rectangle to answer the question:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:

where l is the length and w is the width of the rectangle.
Now, given the rectangle

we can see the length is 9cm and the width is 7cm. So, we can substitute. We get



To find the perimeter of a rectangle, we will use the following formula:
where l is the length and w is the width of the rectangle.
Now, given the rectangle
we can see the length is 9cm and the width is 7cm. So, we can substitute. We get
Compare your answer with the correct one above
What is the perimeter of a square if the side length is  ?
?
What is the perimeter of a square if the side length is 
A square has four congruent sides.
Multiply the quantity by four.

The answer is: 
A square has four congruent sides.
Multiply the quantity by four.
The answer is:
Compare your answer with the correct one above
A rectangular television has a diagonal of  inches and a width of
inches and a width of  inches. What is the area of the television?
inches. What is the area of the television?
A rectangular television has a diagonal of 


The figure above represents the television.
Use the Pythagorean Theorem to find the length of the rectangle.



Next, recall how to find the area of a rectangle.

For the given rectangle,

Make sure to round to two places after the decimal.

The figure above represents the television.
Use the Pythagorean Theorem to find the length of the rectangle.
Next, recall how to find the area of a rectangle.
For the given rectangle,
Make sure to round to two places after the decimal.
Compare your answer with the correct one above

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a quadrilateral?

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a quadrilateral?
By definition, any polygon with four sides is called a quadrilateral. All three figures fit this description.
By definition, any polygon with four sides is called a quadrilateral. All three figures fit this description.
Compare your answer with the correct one above

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a parallelogram?

Refer to the above three figures. All parallel sides are so indicated.
Which of the figures can be called a parallelogram?
A parallelogram, by definition, has two pairs of parallel sides. Figures A and B fit that criterion, but Figure C does not.
A parallelogram, by definition, has two pairs of parallel sides. Figures A and B fit that criterion, but Figure C does not.
Compare your answer with the correct one above
In Rhombus 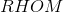 ,
,  . If
. If  is constructed, which of the following is true about
is constructed, which of the following is true about  ?
?
In Rhombus 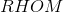



The figure referenced is below.

The sides of a rhombus are congruent by definition, so  , making
, making  isosceles (and possibly equilateral).
isosceles (and possibly equilateral).
Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so
 .
.
 , having measure greater than
, having measure greater than  , is obtuse, making
, is obtuse, making  an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three
an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three  angles.
angles.
The correct response is that  is obtuse and isosceles, but not equilateral.
is obtuse and isosceles, but not equilateral.
The figure referenced is below.

The sides of a rhombus are congruent by definition, so 

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so





The correct response is that 
Compare your answer with the correct one above
Given Quadrilateral  , which of these statements would prove that it is a parallelogram?
, which of these statements would prove that it is a parallelogram?
I)  and
and 
II)  and
and 
III)  and
and  are supplementary and
are supplementary and  and
and  are supplementary
are supplementary
Given Quadrilateral 
I) 
II) 
III) 



Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive.
Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.
Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.
The correct response is Statement II only.
Compare your answer with the correct one above
You are given Parallelogram  with
with  . Which of the following statements, along with what you are given, would be enough to prove that Parallelogram
. Which of the following statements, along with what you are given, would be enough to prove that Parallelogram  is a rectangle?
is a rectangle?
I) 
II) 
III) 
You are given Parallelogram 


I)
II)
III)
A rectangle is defined as a parallelogram with four right, or  , angles.
, angles.
Since opposite angles of a paralellogram are congruent, if one angle measures  , so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total
, so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total  - if one angle measures
- if one angle measures  , then both of the neighboring angles measure
, then both of the neighboring angles measure  .
.
In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
A rectangle is defined as a parallelogram with four right, or 
Since opposite angles of a paralellogram are congruent, if one angle measures 



In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.
Note that the sidelengths are irrelevant.
Compare your answer with the correct one above
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
If the rectangle has a width of 5 and a length of 10, what is the area of the rectangle?
Write the area for a rectangle.

Substitute the given dimensions.

The answer is: 
Write the area for a rectangle.
Substitute the given dimensions.
The answer is:
Compare your answer with the correct one above
In the figure below, find the measure of the largest angle.

In the figure below, find the measure of the largest angle.

Recall that in a quadrilateral, the interior angles must add up to  .
.
Thus, we can solve for  :
:




Now, to find the largest angle, plug in the value of  into each expression for each angle.
into each expression for each angle.




The largest angle is  .
.
Recall that in a quadrilateral, the interior angles must add up to 
Thus, we can solve for 
Now, to find the largest angle, plug in the value of 
The largest angle is 
Compare your answer with the correct one above
Find the area of the trapezoid:

Find the area of the trapezoid:

The area of a trapezoid is calculated using the following equation:

The area of a trapezoid is calculated using the following equation:
Compare your answer with the correct one above
A rectangle has length 10 inches and width 5 inches. Each dimension is increased by 3 inches. By what percent has the area of the rectangle increased?
A rectangle has length 10 inches and width 5 inches. Each dimension is increased by 3 inches. By what percent has the area of the rectangle increased?
The area of a rectangle is its length times its width.
Its original area is  square inches; its new area is
square inches; its new area is  square inches. The area has increased by
square inches. The area has increased by
 .
.
The area of a rectangle is its length times its width.
Its original area is 


Compare your answer with the correct one above
A rectangle has length 10 inches and width 8 inches. Its length is increased by 2 inches, and its width is decreased by 2 inches. By what percent has the area of the rectangle decreased?
A rectangle has length 10 inches and width 8 inches. Its length is increased by 2 inches, and its width is decreased by 2 inches. By what percent has the area of the rectangle decreased?
The area of a rectangle is its length times its width.
Its original area is  square inches; its new area is
square inches; its new area is  square inches. The area has decreased by
square inches. The area has decreased by
 .
.
The area of a rectangle is its length times its width.
Its original area is 


Compare your answer with the correct one above
The length of each side of a square is increased by 10%. By what percent has its area increased?
The length of each side of a square is increased by 10%. By what percent has its area increased?
Let  be the original sidelength of the square. Increasing this by 10% is the same as adding 0.1 times that sidelength to the original sidelength. The new sidelength is therefore
be the original sidelength of the square. Increasing this by 10% is the same as adding 0.1 times that sidelength to the original sidelength. The new sidelength is therefore

The area of a square is the square of its sidelength.
The area of the square was originally  ; it is now
; it is now

That is, the area has increased by
 .
.
Let 
The area of a square is the square of its sidelength.
The area of the square was originally 
That is, the area has increased by

Compare your answer with the correct one above

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely. However, because of the cutting device the pool store uses, the length and the width of the tarp must each be a multiple of four yards. Also, the tarp must be at least one yard longer and one yard wider than the pool.
What will be the minimum area of the tarp the manager purchases?

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely. However, because of the cutting device the pool store uses, the length and the width of the tarp must each be a multiple of four yards. Also, the tarp must be at least one yard longer and one yard wider than the pool.
What will be the minimum area of the tarp the manager purchases?
Three feet make a yard, so the length and width of the pool are  yards and
yards and  yards, respectively. Since the dimensions of the tarp must exceed those of the pool by at least one yard, the tarp must be at least
yards, respectively. Since the dimensions of the tarp must exceed those of the pool by at least one yard, the tarp must be at least  yards by
yards by  yards; but since both dimensions must be multiples of four yards, we take the next multiple of four for each.
yards; but since both dimensions must be multiples of four yards, we take the next multiple of four for each.
The tarp must be 20 yards by 16 yards, so the area of the tarp is the product of these dimensions, or
 square yards.
square yards.
Three feet make a yard, so the length and width of the pool are 



The tarp must be 20 yards by 16 yards, so the area of the tarp is the product of these dimensions, or

Compare your answer with the correct one above