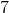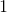Complex Numbers
Complex Analysis · Learn by Concept
Help Questions
Complex Analysis › Complex Numbers
What is the magnitude of the following complex number?
None of these
Explanation
The magnitude of a complex number 
So the modulus of 

Evaluate:
Explanation
The general formula to figure out the modulus is
We apply this to get
Evaluate:
Explanation
The general formula to figure out the modulus is
We apply this to get
What is the magnitude of the following complex number?
None of these
Explanation
The magnitude of a complex number 
So the modulus of 

Evaluate:
Explanation
The general formula to figure out the modulus is
We apply this to get
What is the magnitude of the following complex number?
None of these
Explanation
The magnitude of a complex number 
Because the complex number 



Evaluate
-64
64
64i
-64i
None of the other answers
Explanation
Converting from rectangular to polar coordinates gives us
So
Evaluate:
Explanation
The general formula to figure out the modulus is
We apply this to get
What is the argument of the following complex number?
None of these
Explanation
Note that the complex number 
For a complex number 



where 
Then the argument of 

The angle 



What is the value of 

Not enough information is given.
Explanation
The magnitude of a complex number 

If