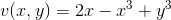Analytic and Harmonic Functions
Complex Analysis · Learn by Concept
Help Questions
Complex Analysis › Analytic and Harmonic Functions
1 - 2
1
Find a Harmonic Conjugate 
CORRECT
Explanation


where 
2
Given 

Nowhere
CORRECT
The Entire Complex Plane
Explanation
Rewriting 
So this implies that
where
Therefore, checking the Cauchy-Riemann Equations, we have that
So the Cauchy-Riemann equations are never satisfied on the entire complex plane, so 
AI Study CoachYour personal study buddy
Instant TutoringConnect with a tutor now
Request a TutorGet matched with an expert
Live ClassesJoin interactive classes
Question of the DayDaily practice to build your skills
FlashcardsStudy and memorize key concepts
WorksheetsBuild custom practice quizzes
AI SolverStep-by-step problem solutions
Learn by ConceptMaster concepts step by step
Diagnostic TestsAssess your knowledge level
Practice TestsTest your skills with exam questions
GamesLearn through free games