Linear Inequalities
College Algebra · Learn by Concept
Help Questions
College Algebra › Linear Inequalities
Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that x is larger than -2. The left-hand term of the interval is -2 since it is the lower bound for our set, and it has a parenthesis around it because it is not included in our set (-2 is not greater than -2). The right-hand term of the interval is positive infinity because any number larger than -2 is in the set. There is always a parenthesis around infinity or negative infinity.
Express the following linear inequality in interval notation.
Explanation
Upon expanding and solving for x, we find that x is greater than -1. The left-hand term of the interval is -1 since it is the lower bound of our set, and has a parenthesis around it because it is not in our set (-1 is not greater than -1). The right-hand term of the interval is infinity because any number larger than -1 is in our set, and there is always a parenthesis around infinity.
Express the following linear inequality in interval notation.
 or
or 
Explanation
Upon solving for x, we find that x is less than or equal to -7/2 OR x is greater than or equal to 1/2. Since x may be in either of those sets, we must take the union of the sets. The first interval begins with negative infinity, since x can be anything less than -7/2. The first interval ends at -7/2 and includes it in the set, so there is a bracket around it. We join this interval with the second interval beginning with 1/2, and there is a bracket around 1/2 since it is in the set. The second interval ends with infinity since any number larger than 1/2 is in our set. There are always parenthesis around infinities.
Solve the following inequality.

Explanation
To solve this inequality, we treat is a a regular equation. First, we add 8 to both sides.

We now divide both sides by 2 to get

Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that 6 is less than x which is less than 7, or that x is greater than 6 AND x is less than 7. The left-hand term of our interval is 6 since it is the lower bound for our set, and there is a parenthesis around it since it is not in our set (6 is not greater than 6). The right-hand term of our interval is 7 since it is the upper bound for our set, and there is a parenthesis around it since it is not in our set (7 is not less than 7). Remember to flip the direction of the inequalities when dividing or multiplying by a negative number.
Express the following linear inequality in interval notation.
 or
or 
Explanation
Upon solving for x, we find that x is less than or equal to -2 OR x is greater than 1. Since x may be in either of those sets, we must take the union of the sets. The first interval begins with negative infinity, since x can be anything less than -2. The first interval ends at -2 and includes it in the set, so there is a bracket around it. We join this interval with the second interval beginning with 1, and there is a parenthesis around 1 since it is not in the set. The second interval ends with infinity since any number larger than 1 is in our set. There are always parenthesis around infinities.
Marvin's Movers charges \$100 plus \$30 per hour to move a household across town. Elliot's Moving Service charges \$55 per hour. For what lengths of time does it cost less to hire Marvin's Movers?
More than 4 hours
Less than 4 hours
More than 5 hours
Less than 5 hours
More than 6 hours
Explanation
Our variable x represents the number of hours to move. Marvin's rate can be expressed as 30x+100. Elliot's rate can be expressed as 55x. We must set the expression for Marvin's rate less than Elliot's rate: 
Solve:
Explanation
To evaluate, we will need to multiply both sides by one-fifth.
The sign does not need to be switched unless we multiply or divide by a negative value.
The answer is:
Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that 8 is less than or equal to x which is less than or equal to 10, or x is greater than or equal to 8 AND x is less than or equal to 10. The left-hand term of our interval is 8 since it is the lower bound for our set, and there is a bracket around it since it is in our set (8 is greater than or equal to 8). The right-hand term of our interval is 10 since it is the upper bound for our set, and there is also a bracket around it since it is in our set (10 is less than or equal to 10).
Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that 1 is less than x which is less than or equal to 5, or x is greater than 1 AND x is less than or equal to 5. The left-hand term of our interval is 1 since it is the lower bound for our set, and there is a parenthesis around it since it is not in our set (1 is not greater than 1). The right-hand term of our interval is 5 since it is the upper bound for our set, and there is a bracket around it since it is in our set (5 is less than or equal to 5). Remember when dividing or multiplying an inequality by a negative number to switch the direction of the inequalities.

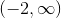
![\left [ -2,\infty \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009903/gif.latex)
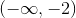







![(-\infty ,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010067/gif.latex)
![(-\infty ,-\frac{7}{2}]\cup[\frac{1}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010360/gif.latex)
![(-\infty ,-\frac{1}{2}]\cup[\frac{7}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010361/gif.latex)
![(-\infty ,-\frac{5}{2}]\cup[\frac{3}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010362/gif.latex)
![(-\infty ,-\frac{3}{2}]\cup[\frac{5}{2},\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010363/gif.latex)
![(-\infty ,-6]\cup[2,\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010364/gif.latex)
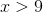
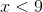

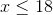



![\left [ 6,7\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010773/gif.latex)

![\left [ -7,-6\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010775/gif.latex)

![(-\infty ,-2]\cup (1,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010355/gif.latex)

![(-\infty ,-1]\cup (2,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010357/gif.latex)

![(-\infty ,-3]\cup (6,\infty )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010359/gif.latex)









![[8,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010205/gif.latex)

![[2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010207/gif.latex)

![(8,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010209/gif.latex)

![(1,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010345/gif.latex)
![[1,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1010346/gif.latex)


