Newtonian Mechanics - AP Physics 1
Card 0 of 4456
A  satellite orbits
satellite orbits  above the Earth. What is the period of the satellite's orbit?
above the Earth. What is the period of the satellite's orbit?



A 

The period describes how long it takes the satellite to make one full orbit. If you go back to the definition of velocity,  , we can apply that to our new circular orbit, in which the distance is equal to the circumference of the circle and the time is equal to the period:
, we can apply that to our new circular orbit, in which the distance is equal to the circumference of the circle and the time is equal to the period:  . The circumference divided by the period will give us the average velocity.
. The circumference divided by the period will give us the average velocity.
The problem gives us the radius, but we need to find the tangential velocity. We can do this by first solving for the centripetal acceleration from the centripetal force.
Recognize that the force due to gravity of the Earth on the satellite is the same as the centripetal force acting on the satellite. That means  .
.
Solve for  for the satellite. To do this, use the law of universal gravitation.
for the satellite. To do this, use the law of universal gravitation.

Remember that  is the distance between the centers of the two objects. That means it will be equal to the radius of the earth PLUS the orbiting distance.
is the distance between the centers of the two objects. That means it will be equal to the radius of the earth PLUS the orbiting distance.
Use the given values for the masses of the objects and distance to solve for the force of gravity.





Now that we know the force, we can find the acceleration. Remember that centripetal force is  . Set our two forces equal and solve for the centripetal acceleration.
. Set our two forces equal and solve for the centripetal acceleration.




Now we can find the tangential velocity, using the equation for centripetal acceleration. Again, remember that the radius is equal to the sum of the radius of the Earth and the height of the satellite!






We now have a value for the tangential velocity, which we can use in the equation for velocity from the beginning to find the period.




The period describes how long it takes the satellite to make one full orbit. If you go back to the definition of velocity, 

The problem gives us the radius, but we need to find the tangential velocity. We can do this by first solving for the centripetal acceleration from the centripetal force.
Recognize that the force due to gravity of the Earth on the satellite is the same as the centripetal force acting on the satellite. That means 
Solve for 
Remember that 
Use the given values for the masses of the objects and distance to solve for the force of gravity.
Now that we know the force, we can find the acceleration. Remember that centripetal force is 
Now we can find the tangential velocity, using the equation for centripetal acceleration. Again, remember that the radius is equal to the sum of the radius of the Earth and the height of the satellite!
We now have a value for the tangential velocity, which we can use in the equation for velocity from the beginning to find the period.
Compare your answer with the correct one above
A  satellite orbits
satellite orbits  above the Earth. The satellite runs into another stationary satellite of equal mass and the two stick together. What is their resulting velocity?
above the Earth. The satellite runs into another stationary satellite of equal mass and the two stick together. What is their resulting velocity?



A 

We can use the conservation of momentum to solve. Since the satellites stick together, there is only one final velocity term.

We know the masses for both satellites are equal, and the second satellite is initially stationary.

Now we need to find the velocity of the first satellite. Since the satellite is in orbit (circular motion), we need to find the tangential velocity. We can do this by finding the centripetal acceleration from the centripetal force.
Recognize that the force due to gravity of the Earth on the satellite is the same as the centripetal force acting on the satellite. That means  .
.
Solve for  for the satellite. To do this, use the law of universal gravitation.
for the satellite. To do this, use the law of universal gravitation.

Remember that  is the distance between the centers of the two objects. That means it will be equal to the radius of the earth PLUS the orbiting distance.
is the distance between the centers of the two objects. That means it will be equal to the radius of the earth PLUS the orbiting distance.
Use the given values for the masses of the objects and distance to solve for the force of gravity.





Now that we know the force, we can find the acceleration. Remember that centripetal force is  . Set our two forces equal and solve for the centripetal acceleration.
. Set our two forces equal and solve for the centripetal acceleration.




Now we can find the tangential velocity, using the equation for centripetal acceleration. Again, remember that the radius is equal to the sum of the radius of the Earth and the height of the satellite!






This value is the tangential velocity, or the initial velocity of the first satellite. We can plug this into the equation for conversation of momentum to solve for the final velocity of the two satellites.





We can use the conservation of momentum to solve. Since the satellites stick together, there is only one final velocity term.
We know the masses for both satellites are equal, and the second satellite is initially stationary.
Now we need to find the velocity of the first satellite. Since the satellite is in orbit (circular motion), we need to find the tangential velocity. We can do this by finding the centripetal acceleration from the centripetal force.
Recognize that the force due to gravity of the Earth on the satellite is the same as the centripetal force acting on the satellite. That means 
Solve for 
Remember that 
Use the given values for the masses of the objects and distance to solve for the force of gravity.
Now that we know the force, we can find the acceleration. Remember that centripetal force is 
Now we can find the tangential velocity, using the equation for centripetal acceleration. Again, remember that the radius is equal to the sum of the radius of the Earth and the height of the satellite!
This value is the tangential velocity, or the initial velocity of the first satellite. We can plug this into the equation for conversation of momentum to solve for the final velocity of the two satellites.
Compare your answer with the correct one above
One car with a mass of 400kg is traveling east at  and collides with a car of mass 800kg traveling west at
and collides with a car of mass 800kg traveling west at  . Assuming the collision is completely inellastic, what is velocity of the first car after the collision?
. Assuming the collision is completely inellastic, what is velocity of the first car after the collision?
One car with a mass of 400kg is traveling east at 

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:

There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:

Rearranging for final velocity, we get:

At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:


Since this value is positive, the final answer is  West.
West.
Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:
There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:
Rearranging for final velocity, we get:
At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:
Since this value is positive, the final answer is 
Compare your answer with the correct one above
"A box traveling on a slippery surface will continue at its initial speed forever." This statement is consistent with which law?
"A box traveling on a slippery surface will continue at its initial speed forever." This statement is consistent with which law?
The correct answer is "Newton's First Law: every object continues in its state of rest or of uniform velocity in a straight line as long as no net force acts on it." On a slippery surface, we can assume there is no friction. If there is no friction working against the box's movement, the box will continue to move at its initial velocity forever. If the box were on a rough surface, friction from the surface would act against the box, causing the box's velocity to slow and eventually stop (if the force acting on the box is not greater than that of the frictional force).
The correct answer is "Newton's First Law: every object continues in its state of rest or of uniform velocity in a straight line as long as no net force acts on it." On a slippery surface, we can assume there is no friction. If there is no friction working against the box's movement, the box will continue to move at its initial velocity forever. If the box were on a rough surface, friction from the surface would act against the box, causing the box's velocity to slow and eventually stop (if the force acting on the box is not greater than that of the frictional force).
Compare your answer with the correct one above
An object rests in the middle of an empty, motionless boxcar on a perfectly frictionless surface.
What will happen when the boxcar is pulled forward by a locomotive?
An object rests in the middle of an empty, motionless boxcar on a perfectly frictionless surface.
What will happen when the boxcar is pulled forward by a locomotive?
According to Newton's first law, an object will remain at rest until a force is applied. If the floor of the boxcar is perfectly motionless, than the object will remain in the same spot in relation to the earth. This will make it appear to move to the back of the boxcar.
According to Newton's first law, an object will remain at rest until a force is applied. If the floor of the boxcar is perfectly motionless, than the object will remain in the same spot in relation to the earth. This will make it appear to move to the back of the boxcar.
Compare your answer with the correct one above
How much force must be applied to keep an object with a mass of  moving to the left at a constant velocity of
moving to the left at a constant velocity of  ?
?
How much force must be applied to keep an object with a mass of 

Force is defined as

Since the velocity is constant, the acceleration is zero. Therefore the force required to keep this object in motion is zero.
This is also stated in Newton's First Law: "An object will remain at rest or in uniform motion in a straight line unless acted upon by an external force."
Force is defined as
Since the velocity is constant, the acceleration is zero. Therefore the force required to keep this object in motion is zero.
This is also stated in Newton's First Law: "An object will remain at rest or in uniform motion in a straight line unless acted upon by an external force."
Compare your answer with the correct one above
A van is driving around with a bowling ball in the back, free to roll around. The van approaches a red light and must decelerate to come to a complete stop. As the van is slowing down, which direction is the bowling ball rolling?
A van is driving around with a bowling ball in the back, free to roll around. The van approaches a red light and must decelerate to come to a complete stop. As the van is slowing down, which direction is the bowling ball rolling?
According to Newton's First Law of Motion, an object that is in motion will stay in motion unless acted on by another force. When the van slows down, the ball will want to continue moving forward, and the friction between it and the floor of the van is not strong enough to keep the ball back.
According to Newton's First Law of Motion, an object that is in motion will stay in motion unless acted on by another force. When the van slows down, the ball will want to continue moving forward, and the friction between it and the floor of the van is not strong enough to keep the ball back.
Compare your answer with the correct one above
A 2000kg car with a velocity of  collides head on with a 6000kg truck with a velocity of
collides head on with a 6000kg truck with a velocity of  . Which vehicle experiences the greater force? Which experiences the greater acceleration?
. Which vehicle experiences the greater force? Which experiences the greater acceleration?
A 2000kg car with a velocity of 

The car and the truck experience equal and opposite forces, but since the car has a smaller mass it will experience greater acceleration than the truck according to the equation F = ma.

A greater mass will decrease the acceleration.
The car and the truck experience equal and opposite forces, but since the car has a smaller mass it will experience greater acceleration than the truck according to the equation F = ma.
A greater mass will decrease the acceleration.
Compare your answer with the correct one above
A popular topic in early space exploration was how to safely return modules back to the surface of the earth. Early designs contained materials that could only withstand impulses of up to  before parts of the module became compromised. One such model of mass 500kg is approaching ocean waters and deploys its shoot, reducing its speed to
before parts of the module became compromised. One such model of mass 500kg is approaching ocean waters and deploys its shoot, reducing its speed to  . If the module decelerates to zero velocity in 0.9 seconds upon hitting the water, is the module structurally compromised?
. If the module decelerates to zero velocity in 0.9 seconds upon hitting the water, is the module structurally compromised?

A popular topic in early space exploration was how to safely return modules back to the surface of the earth. Early designs contained materials that could only withstand impulses of up to 

We need to use the equation for impulse to solve this problem. In fact, the time given is completely irrevelevant:

Plugging in our values:

This is less than the threshold, so no, nothing becomes structurally compromised
We need to use the equation for impulse to solve this problem. In fact, the time given is completely irrevelevant:
Plugging in our values:
This is less than the threshold, so no, nothing becomes structurally compromised
Compare your answer with the correct one above
In a billiards game, one player hits the cue ball towards another ball. The cue ball has a mass of 0.1kg and hits the other ball with a velocity of  . If the collision is completely elastic and the cue ball travels with a velocity of
. If the collision is completely elastic and the cue ball travels with a velocity of  after the collision, what is the mass and velocity of the other ball?
after the collision, what is the mass and velocity of the other ball?
In a billiards game, one player hits the cue ball towards another ball. The cue ball has a mass of 0.1kg and hits the other ball with a velocity of 

Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:


Rearrange the first equation for  and the second for
and the second for  .
.


We can rewrite the second equation as:

Substitute our equation for  into the second equation:
into the second equation:

Rearranging, we get:



Plug in our values for the initial and final velocities:


To solve for mass, we'll use our earlier expression for  :
:


Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:
Rearrange the first equation for 

We can rewrite the second equation as:
Substitute our equation for 
Rearranging, we get:
Plug in our values for the initial and final velocities:
To solve for mass, we'll use our earlier expression for 
Compare your answer with the correct one above
A marble of mass  falls off a bed with a height of
falls off a bed with a height of  . What is the impulse on the marble as it hits the ground?
. What is the impulse on the marble as it hits the ground?

A marble of mass 

Impulse can be written as either of two popular expressions:

From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:

Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:

Canceling out mass and rearranging for final velocity, we get:

We know these variables, allowing us to solve for the velocity:

Plugging this value into the expression for impulse, we get:

Impulse can be written as either of two popular expressions:
From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:
Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:
Canceling out mass and rearranging for final velocity, we get:
We know these variables, allowing us to solve for the velocity:
Plugging this value into the expression for impulse, we get:
Compare your answer with the correct one above
Two astronauts in space are traveling directly towards each other. Astronaut A has a mass of  and a velocity of
and a velocity of  and Astronaut B has a mass of
and Astronaut B has a mass of  and a velocity of
and a velocity of  . When the astronauts collide, they grab onto each other. What is the velocity of the two astronauts after the collision as they continue to grab onto each other?
. When the astronauts collide, they grab onto each other. What is the velocity of the two astronauts after the collision as they continue to grab onto each other?
Two astronauts in space are traveling directly towards each other. Astronaut A has a mass of 



Momentum is always conserved. Equation for conservation of momentum:

There is only one velocity on the right since the two astronauts grab onto each other, thus they move together at the same velocity. Solve.


Momentum is always conserved. Equation for conservation of momentum:
There is only one velocity on the right since the two astronauts grab onto each other, thus they move together at the same velocity. Solve.
Compare your answer with the correct one above
Tom drops a ball of mass  from rest from a height
from rest from a height  . The ball bounces back to a height of
. The ball bounces back to a height of  . Find the magnitude of the impulse the ground imparted on the ball.
. Find the magnitude of the impulse the ground imparted on the ball.
Tom drops a ball of mass 


Impulse is just the change in momentum. To find the velocity when the ball hits the ground, we need to use kinematics. We know the height the ball is dropped, the acceleration, and the initial velocity, so we can use the equation  . The initial velocity is
. The initial velocity is  ,
,  , and
, and  , so the equation becomes
, so the equation becomes 

When the ball bounces back up it reaches a height of  . In order to find the velocity immediately after it hits the ground, we can use the same equation with
. In order to find the velocity immediately after it hits the ground, we can use the same equation with  . This will lead it a velocity of
. This will lead it a velocity of 
Assuming up is positive, the magnitude of the impulse is just 
Impulse is just the change in momentum. To find the velocity when the ball hits the ground, we need to use kinematics. We know the height the ball is dropped, the acceleration, and the initial velocity, so we can use the equation 



When the ball bounces back up it reaches a height of 

Assuming up is positive, the magnitude of the impulse is just
Compare your answer with the correct one above
Consider the following system:
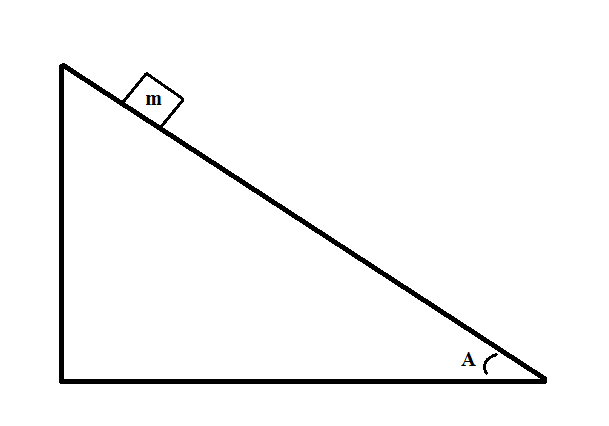
If the block has a mass of  , the angle measures
, the angle measures  , and there is no friction between the block and slope, what is the momentum of the block after it has traveled a horizontal distance of
, and there is no friction between the block and slope, what is the momentum of the block after it has traveled a horizontal distance of  ?
?
Consider the following system:

If the block has a mass of 


To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:

If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:

Substituting expressions for each term, we get:

Cancel out mass and rearrange to solve for velocity:

We can use the horizontal distance traveled and the angle of the slope to determine the initial height:



Now that we have the initial height, we can solve for final velocity:

Finally, we can now use the equation for momentum to solve the problem:



To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:
If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:
Substituting expressions for each term, we get:
Cancel out mass and rearrange to solve for velocity:
We can use the horizontal distance traveled and the angle of the slope to determine the initial height:
Now that we have the initial height, we can solve for final velocity:
Finally, we can now use the equation for momentum to solve the problem:
Compare your answer with the correct one above
If the velocity of an objects is halved, what is the resulting change in the kinetic energy?
If the velocity of an objects is halved, what is the resulting change in the kinetic energy?
The equation for kinetic energy is:
 , where
, where  is the velocity of the object. Therefore, if we halve the velocity, we can substitute that into our equation, and see what will change in the kinetic energy equation:
is the velocity of the object. Therefore, if we halve the velocity, we can substitute that into our equation, and see what will change in the kinetic energy equation:

Thus, the kinetic energy is quartered.
The equation for kinetic energy is:


Thus, the kinetic energy is quartered.
Compare your answer with the correct one above
A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?
A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?
To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.
There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.




To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.
There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.
Compare your answer with the correct one above
A homogenous mass of 0.25kg is fixed to a 0.5kg Hookean spring. When the mass/spring system is stretched 1cm from the equilibrium, it takes 3N of force to hold the mass in place. If the displacement from equilibrium is doubled, the force necessary to keep the system in place will .
A homogenous mass of 0.25kg is fixed to a 0.5kg Hookean spring. When the mass/spring system is stretched 1cm from the equilibrium, it takes 3N of force to hold the mass in place. If the displacement from equilibrium is doubled, the force necessary to keep the system in place will .
Since the spring is Hookean, the relationship between the force and displacement from equilibrium of the mass can be expressed by Hooke's Law:

Since this equation is linear, the force and displacement are directly proportional. Thus, when the displacement doubles, the force doubles.
Since the spring is Hookean, the relationship between the force and displacement from equilibrium of the mass can be expressed by Hooke's Law:
Since this equation is linear, the force and displacement are directly proportional. Thus, when the displacement doubles, the force doubles.
Compare your answer with the correct one above
A submarine launches a missile from underwater. The missile passes through the surface of the sea at a velocity of  . At this point, a thruster ignites, causing the missile to accelerate in a straight line at
. At this point, a thruster ignites, causing the missile to accelerate in a straight line at  . After 10 seconds of acceleration, how far has the missile traveled?
. After 10 seconds of acceleration, how far has the missile traveled?
A submarine launches a missile from underwater. The missile passes through the surface of the sea at a velocity of 

We need our kinematic equation that relates displacement, initial velocity, and acceleration:

We can neglect gravity in this problem since the statement says that the missile accelerates in a straight line at a constant rate.
Plugging in our values, we get:


We need our kinematic equation that relates displacement, initial velocity, and acceleration:
We can neglect gravity in this problem since the statement says that the missile accelerates in a straight line at a constant rate.
Plugging in our values, we get:
Compare your answer with the correct one above
A cannon is packed with gunpowder and a ball of mass 10kg. The cannon is angled at 30 degrees. When fired, the gunpowder releases 500J of energy, which is all transferred to the cannon ball. Neglecting air resistance and friction within the cannon, how far does the ball travel before hitting the ground?
Assume 
A cannon is packed with gunpowder and a ball of mass 10kg. The cannon is angled at 30 degrees. When fired, the gunpowder releases 500J of energy, which is all transferred to the cannon ball. Neglecting air resistance and friction within the cannon, how far does the ball travel before hitting the ground?
Assume
There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.
Method 1: Range Equation
The range equation is the following:

We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:

Rearranging for velocity:

Now we can plug everything into the range equation:

Method 2: Kinematics Equations
As in the first method, we can calculate the initial velocity of the ball:

Rearranging for velocity:

We can then split this into it's components:


We can use the y-component to calculate how long the ball is in the air. We can do one of two things:
- Calculate how long the ball takes to reach it's peak and then multiply by 2
- Calculate how lon gthe ball takes to get a velocity of -5
We'll go with method 2:

Rearranging for t:


Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).

There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.
Method 1: Range Equation
The range equation is the following:
We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:
Rearranging for velocity:
Now we can plug everything into the range equation:
Method 2: Kinematics Equations
As in the first method, we can calculate the initial velocity of the ball:
Rearranging for velocity:
We can then split this into it's components:
We can use the y-component to calculate how long the ball is in the air. We can do one of two things:
- Calculate how long the ball takes to reach it's peak and then multiply by 2
- Calculate how lon gthe ball takes to get a velocity of -5
We'll go with method 2:
Rearranging for t:
Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).
Compare your answer with the correct one above
A passenger jet is beginning its decent to its final destination. If it is at a height of 3,000m and traveling at a rate of  , what should be its angle of decent to arrive in 10 minutes?
, what should be its angle of decent to arrive in 10 minutes?
A passenger jet is beginning its decent to its final destination. If it is at a height of 3,000m and traveling at a rate of 
We know that the plane needs to drop 3,000 meters in 10 minutes. Therefore, we can calculate the vertical velocity that the plane needs to be traveling at:

Knowing the plane's velocity, we can caluclate what angle at which it needs to decend to achieve this vertical velocity:

Rearranging for theta:

Plugging in our values:

We know that the plane needs to drop 3,000 meters in 10 minutes. Therefore, we can calculate the vertical velocity that the plane needs to be traveling at:
Knowing the plane's velocity, we can caluclate what angle at which it needs to decend to achieve this vertical velocity:
Rearranging for theta:
Plugging in our values:
Compare your answer with the correct one above