Linear Equations - Algebra
Card 0 of 11961
Solve 
Solve
Solving for a one-step linear equation is simple. All you're being asked is to solve for x. In other words, how do you get x by itself on one side of the equals sign?
In order to solve for these kind of problems, it's important to keep in mind that what you do to one side must be done to the other.
for  , we want to get x by itself. The fastest way would be to move the
, we want to get x by itself. The fastest way would be to move the  from left of the equals sign to the right with
from left of the equals sign to the right with  .
.
This can be accomplished by subtracting  from both sides.
from both sides.



Solving for a one-step linear equation is simple. All you're being asked is to solve for x. In other words, how do you get x by itself on one side of the equals sign?
In order to solve for these kind of problems, it's important to keep in mind that what you do to one side must be done to the other.
for 


This can be accomplished by subtracting 
Compare your answer with the correct one above
Solve for  :
:

Solve for 
Subtract 53 from each side of the equation to get  by itself:
by itself:


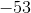
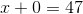

Subtract 53 from each side of the equation to get 

Compare your answer with the correct one above
Evaluate the expression (3x + 4y)3 when x = 4 and y = 2.
Evaluate the expression (3x + 4y)3 when x = 4 and y = 2.
Plug in 4 for x and 2 for y, giving you (3(4) + 4(2))3, which equals (20)3, equalling 8000.
(3x + 4y)3
(3(4) + 4(2))3
(12 + 8)3
(20)3 = 8000
Plug in 4 for x and 2 for y, giving you (3(4) + 4(2))3, which equals (20)3, equalling 8000.
(3x + 4y)3
(3(4) + 4(2))3
(12 + 8)3
(20)3 = 8000
Compare your answer with the correct one above
Evaluate  when x = 3.
when x = 3.
Evaluate 
First plug 3 in for x, giving you  . You square 6, giving you 36, then subtract (18/2), giving you 27.
. You square 6, giving you 36, then subtract (18/2), giving you 27.




First plug 3 in for x, giving you 
Compare your answer with the correct one above
Express the sum of  and
and  is forty.
is forty.
Express the sum of 

Take every word and translate into math. Sum is addition. Is means equal sign. So we have  .
.
Take every word and translate into math. Sum is addition. Is means equal sign. So we have 
Compare your answer with the correct one above
Solve for  .
.

Solve for 

Add 5 to each side of the equation.

Add 3x to each side of the equation.

Divide each side of the equation by 5.

Add 5 to each side of the equation.
Add 3x to each side of the equation.
Divide each side of the equation by 5.
Compare your answer with the correct one above
Solve for  .
.

Solve for 

Subtract 9 from both sides of the equation.

Divide each side of the equation by 3.


Subtract 9 from both sides of the equation.
Divide each side of the equation by 3.
Compare your answer with the correct one above
Solve for  .
.

Solve for 
Let's cross multiply.

We have
 .
.
Divide both sides by  , we get
, we get
 .
.
Let's cross multiply.
We have

Divide both sides by 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
Let's cross multiply.

We have
 .
.
Divide both sides by  , we get
, we get
 .
.
Let's cross multiply.
We have

Divide both sides by 

Compare your answer with the correct one above
Solve for  :
:

Solve for 
Let's cross multiply.

We have
 .
.
Divide both sides by  , we have
, we have
 .
.
Let's cross multiply.
We have

Divide both sides by 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
Let's cross multiply.

We have
 .
.
Divide both sides by  , we have
, we have
 .
.
Let's cross multiply.
We have

Divide both sides by 

Compare your answer with the correct one above
Solve for  .
.

Solve for 
Let's cross multiply and distribute the  .
.


We have  .
.
Subtract both sides by  and divide both sides by
and divide both sides by  .
.



Let's cross multiply and distribute the 
We have 
Subtract both sides by 

Compare your answer with the correct one above
Absolute value symbols tell you to take whatever number is inside the absolute value and make it positive. This is important to remember for equations with variables like x because if the variable is inside the absolute value symbols, that means two values for the variable will give the right answer. You solve for both the positive and the negative of whatever number is on the other side of the equation, since the absolute value symbols will turn both positive and negative numbers into positive ones. For example, in this problem, the absolute value of 2x+4 is alone on one side of the equation with a variable (x) in it. Set 2x+4 equal to both 16 and -16 in two different equations removing the absolute value sign.
You should have  and
and  . Solve to get x alone.
. Solve to get x alone.
Subtract 4 from both sides of the equation to get
 and
and 
Divide by 2 on both sides of the equation to get
 and
and 
If you want to check these answers plug them back into the original equation.




Now try the other solution.




Both solutions for x check out to give the answer 16.
Absolute value symbols tell you to take whatever number is inside the absolute value and make it positive. This is important to remember for equations with variables like x because if the variable is inside the absolute value symbols, that means two values for the variable will give the right answer. You solve for both the positive and the negative of whatever number is on the other side of the equation, since the absolute value symbols will turn both positive and negative numbers into positive ones. For example, in this problem, the absolute value of 2x+4 is alone on one side of the equation with a variable (x) in it. Set 2x+4 equal to both 16 and -16 in two different equations removing the absolute value sign.
You should have 

Subtract 4 from both sides of the equation to get

Divide by 2 on both sides of the equation to get

If you want to check these answers plug them back into the original equation.
Now try the other solution.
Both solutions for x check out to give the answer 16.
Compare your answer with the correct one above
Solve the equation: 
Solve the equation:
Isolate the  by subtracting
by subtracting  on both sides.
on both sides.

Simplify both sides.
The answer is: 
Isolate the 

Simplify both sides.
The answer is:
Compare your answer with the correct one above
Solve the equation: 
Solve the equation:
To isolate the x-variable, we will need to add 17 on both sides.

When adding a positive number with a negative number, the final number will be closer to zero.
Simplify both sides.
The answer is: 
To isolate the x-variable, we will need to add 17 on both sides.
When adding a positive number with a negative number, the final number will be closer to zero.
Simplify both sides.
The answer is:
Compare your answer with the correct one above
Solve the equation: 
Solve the equation:
In order to isolate the variable, add 55 on both sides.

Simplify both sides of the equation.

The answer is: 
In order to isolate the variable, add 55 on both sides.
Simplify both sides of the equation.
The answer is:
Compare your answer with the correct one above
Solve the equation: 
Solve the equation:
To isolate the x-variable, divide both sides by six.

Cancel the sixes on the left and rewrite the right side using common factors.

Cancel the threes.
The answer is: 
To isolate the x-variable, divide both sides by six.
Cancel the sixes on the left and rewrite the right side using common factors.
Cancel the threes.
The answer is:
Compare your answer with the correct one above
This problem should be easy if you have a basic understanding of absolute values. Knowing that absolute values make whatever numbers inside them positive, ask yourself, what values for x will equal positive or negative 9? You can again set up two equations.
 and
and 
These two equations are already solved for x which means we have our answers.
Double checking by plugging these back into the original equation...
Plugging in 9.


Now to try plugging in -9.



Both answers check out
This problem should be easy if you have a basic understanding of absolute values. Knowing that absolute values make whatever numbers inside them positive, ask yourself, what values for x will equal positive or negative 9? You can again set up two equations.

These two equations are already solved for x which means we have our answers.
Double checking by plugging these back into the original equation...
Plugging in 9.
Now to try plugging in -9.
Both answers check out
Compare your answer with the correct one above
Convert 16 quarts into gallons.
Convert 16 quarts into gallons.
To solve this conversion we have to remember that there are 4 quarts per 1 gallon.
In order to have gallons left as our unit, we need to make sure that the other units cancel out by one being in the numerator and one being in the denominator.
Therefore, set up the following conversion and solve:

To solve this conversion we have to remember that there are 4 quarts per 1 gallon.
In order to have gallons left as our unit, we need to make sure that the other units cancel out by one being in the numerator and one being in the denominator.
Therefore, set up the following conversion and solve:
Compare your answer with the correct one above
Harold has a (full) two liter bottle of soda in his refrigerator. He takes it out and pours eight-ounce glasses of soda for himself and each of his three friends that have come over. How many liters of soda are left in the bottle (rounded to two decimal places)?
1 liter = 33.814 fluid ounces
Harold has a (full) two liter bottle of soda in his refrigerator. He takes it out and pours eight-ounce glasses of soda for himself and each of his three friends that have come over. How many liters of soda are left in the bottle (rounded to two decimal places)?
1 liter = 33.814 fluid ounces
Convert the two liters of soda into ounces.

Subtract the four eight-ounce glasses of soda that were poured.

Convert the remaining ounces back into liters.

Alternatively, you could set it up as one equation and solve for  , as shown below.
, as shown below.
![x = 2 - [(8\times 4)\times\tfrac{1}{33.814}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26660/gif.latex)


Convert the two liters of soda into ounces.
Subtract the four eight-ounce glasses of soda that were poured.
Convert the remaining ounces back into liters.
Alternatively, you could set it up as one equation and solve for 
Compare your answer with the correct one above

