Polynomial Functions
Algebra 2 · Learn by Concept
Help Questions
Algebra 2 › Polynomial Functions
For the graph below, match the graph b with one of the following equations:




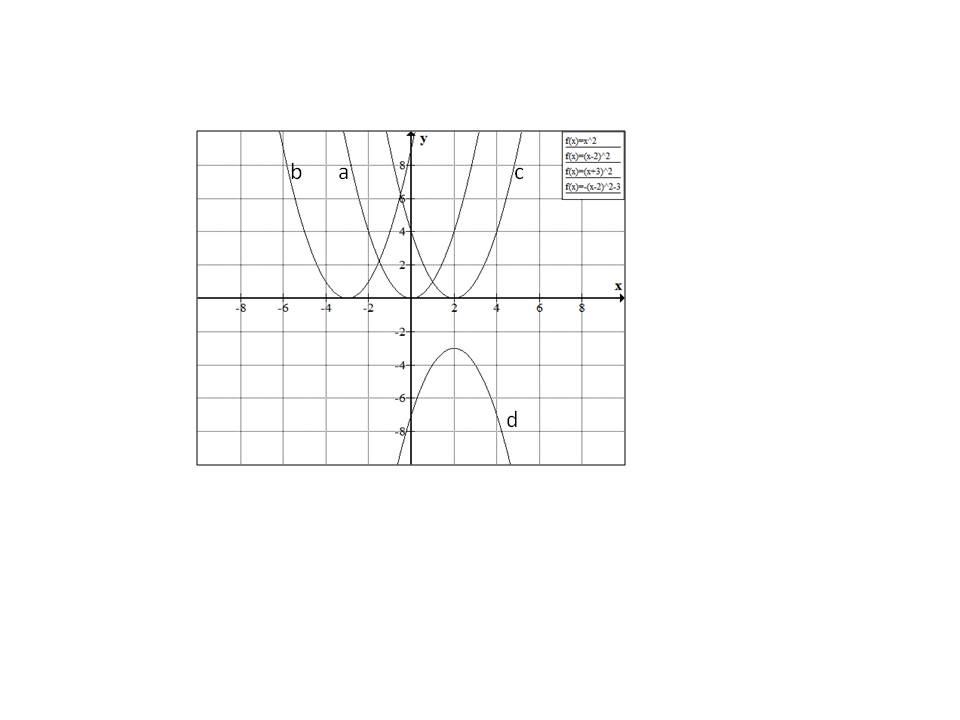




None of the above
Explanation
Starting with



Similarly 

Hence the correct answer is option 
What transformations have been enacted upon 

vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 6 units right
Explanation
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
For the graph below, match the graph b with one of the following equations:









None of the above
Explanation
Starting with



Similarly 

Hence the correct answer is option 
What transformations have been enacted upon 

vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 6 units right
Explanation
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
Let 



Explanation
When solving functions within functions, we begin with the innermost function and work our way outwards. Therefore:
and
Let 



Explanation
When solving functions within functions, we begin with the innermost function and work our way outwards. Therefore:
and
Let ![\small f(x)=\sqrt[3]{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215102/gif.latex)

![\small h(x)=\sqrt[4]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215104/gif.latex)

Explanation
This problem relies on our knowledge of a radical expression ![\small \sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215106/gif.latex)

and
Let ![\small f(x)=\sqrt[3]{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215102/gif.latex)

![\small h(x)=\sqrt[4]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215104/gif.latex)

Explanation
This problem relies on our knowledge of a radical expression ![\small \sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215106/gif.latex)

and
Write the transformation of the given function flipped, and moved one unit to the left:
Explanation
To transform a function horizontally, we must add or subtract the units we transform to x directly. To move left, we add units to x, which is opposite what one thinks should happen, but keep in mind that to move left is to be more negative. To flip a function, the entire function changes in sign.
After making both of these changes, we get
Shift 
Explanation
We will need to determine the equation of the parabola in standard form, which is:
Use the FOIL method to expand the binomials.
Shifting this up two units will add two to the value of 
The answer is:






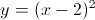




![g(x)=4[2(x-3)]^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/155687/gif.latex)








![\small \sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215072/gif.latex)
![\small \sqrt[4]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215073/gif.latex)
![\small \sqrt[3]{x^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215074/gif.latex)
![\small \sqrt[4]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215075/gif.latex)
![\small g(h(x))=(\sqrt[4]{x})^3=x^\frac{3}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215108/gif.latex)
![\small f(g(h(x)))=\sqrt[3]{(x^\frac{3}{4})^2}=\sqrt[3]{x^\frac{6}{4}}=x^\frac{6}{12}=x^\frac{1}{2}=\sqrt{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/215109/gif.latex)

![-[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702384/gif.latex)
![-[(x-1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702385/gif.latex)
![[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702386/gif.latex)
![[(x-1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702387/gif.latex)
![-[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702536/gif.latex)







