Graphing Logarithmic Functions
Algebra 2 · Learn by Concept
Help Questions
Algebra 2 › Graphing Logarithmic Functions
Give the 
to two decimal places.
The graph has no 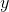
Explanation
Set 
The 

Give the 
to two decimal places.
The graph has no 
Explanation
Set 
The 

What is/are the asymptote(s) of the graph of the function 


Explanation
The graph of the logarithmic function
has as its only asymptote the vertical line
Here, since 

Which is true about the graph of

All of the answers are correct
The domain of the function is greater than zero
The range of the function is infinite in both directions positive and negative.
When 

None of the answers are correct
Explanation
There is no real number 
Therefore in the equation 

However, 
Finally, when 

Which of the following is true about the graph of
The graph is the mirror image of 
The domain is infinite in both directions.
The range must be greater than zero.
It is an even function.
It is an odd function.
Explanation


Give the equation of the horizontal asymptote of the graph of the equation

The graph of 
Explanation
Let
In terms of 
This is the graph of 
The graph of 

Find the equation of the vertical asymptote of the graph of the equation

Explanation
Let 


The graph of 
















































