Functions and Graphs - Algebra 2
Card 1 of 2484
Given the above circle inequality, is the shading on the graph inside or outside the circle?
Given the above circle inequality, is the shading on the graph inside or outside the circle?
Tap to reveal answer
Check the center of the circle to see if that point satisfies the inequality. When evaluating the function at the center (-2,4), we see that it does not satisfy the equation, so it cannot be in the shaded region of the graph. Therefore the shading is outside of the circle.
Check the center of the circle to see if that point satisfies the inequality. When evaluating the function at the center (-2,4), we see that it does not satisfy the equation, so it cannot be in the shaded region of the graph. Therefore the shading is outside of the circle.
← Didn't Know|Knew It →
True or false: The graph of 
has as a horizontal asymptote the graph of the equation 
.
True or false: The graph of
Tap to reveal answer
is a rational function in simplest form whose denominator has a polynomial with degree greater than that of the polynomial in its numerator (2 and 1, respectively). The graph of such a function has as its horizontal asymptote the line of the equation 
.
← Didn't Know|Knew It →
Which of the following is an equation perpendicular to a horizontal line?
Which of the following is an equation perpendicular to a horizontal line?
Tap to reveal answer
The horizontal line will have a slope of 
in the form of 
.
Recall that perpendicular lines have a slope that is the negative reciprocal of the original slope.
This indicates that the vertical line will have undefined slope. Vertical lines have a fixed x-value that will not change.
The answer that is perpendicular to a horizontal line cannot have a y-variable in the equation.
The equation 
represents a pair of intersecting lines.
The only possible answer is: 
The horizontal line will have a slope of
Recall that perpendicular lines have a slope that is the negative reciprocal of the original slope.
This indicates that the vertical line will have undefined slope. Vertical lines have a fixed x-value that will not change.
The answer that is perpendicular to a horizontal line cannot have a y-variable in the equation.
The equation
The only possible answer is:
← Didn't Know|Knew It →
Tap to reveal answer
All inputs are valid. There is nothing you can put in for x that won't work.
All inputs are valid. There is nothing you can put in for x that won't work.
← Didn't Know|Knew It →
What is the domain? 
What is the domain?
Tap to reveal answer
Notice that this is a parabolic function that will open downward. The domain refers to all possible x-values on the graph.
The parent function 
has a domain of all real numbers and a range from 
. The transformations of 
will not affect the domain, but the range of the graph since the y-values of the graph are affected.
There are no values of the x-variable that will make this function undefined, which means all real numbers can exist.
The answer is: 
Notice that this is a parabolic function that will open downward. The domain refers to all possible x-values on the graph.
The parent function
There are no values of the x-variable that will make this function undefined, which means all real numbers can exist.
The answer is:
← Didn't Know|Knew It →
Tap to reveal answer
All inputs are valid. There is nothing you can put in for x that won't work.
All inputs are valid. There is nothing you can put in for x that won't work.
← Didn't Know|Knew It →
Which equation best represents the following graph?
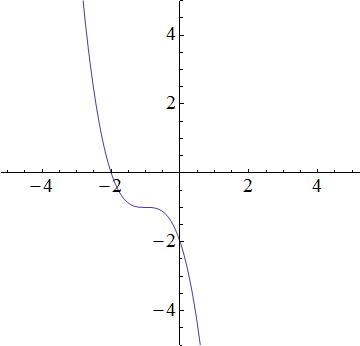
Which equation best represents the following graph?
Tap to reveal answer
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
← Didn't Know|Knew It →
For the graph below, match the graph b with one of the following equations:
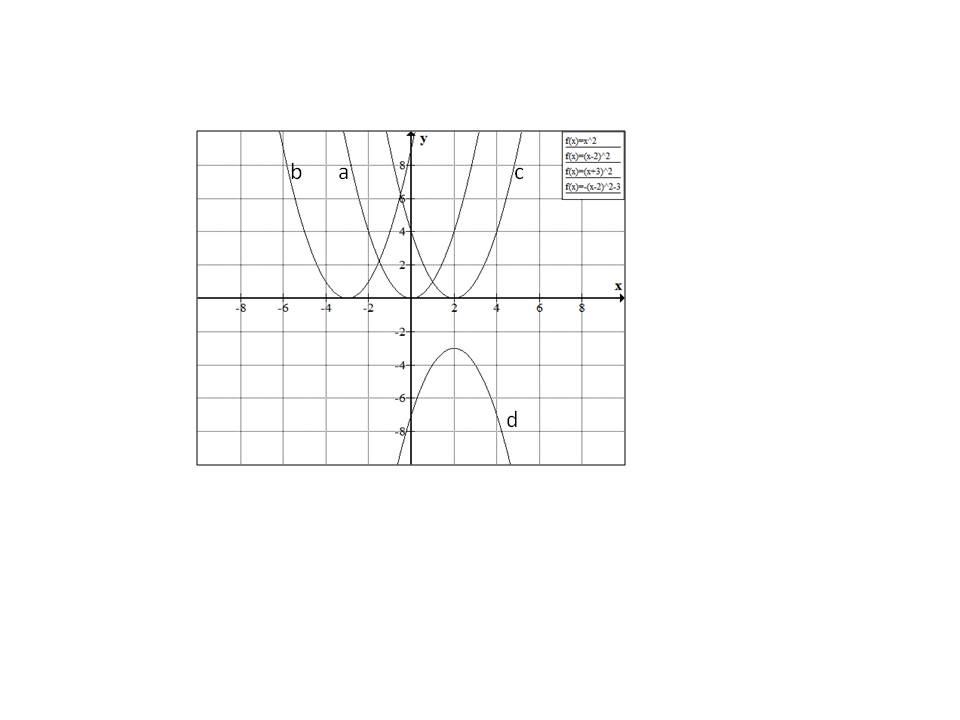
For the graph below, match the graph b with one of the following equations:
Tap to reveal answer
Starting with 
moves the parabola 
by 
units to the right.
Similarly 
moves the parabola by 
units to the left.
Hence the correct answer is option 
.
Starting with
Similarly
Hence the correct answer is option
← Didn't Know|Knew It →
Tap to reveal answer
You cannot take the square root of a negative number.
You cannot take the square root of a negative number.
← Didn't Know|Knew It →
Tap to reveal answer
The function includes all possible y-values (outputs). There is nothing you can put in for y that won't work.
The function includes all possible y-values (outputs). There is nothing you can put in for y that won't work.
← Didn't Know|Knew It →
Tap to reveal answer
Squaring an input cannot produce a negative output.
Squaring an input cannot produce a negative output.
← Didn't Know|Knew It →
Which of the graphs best represents the following function?
Which of the graphs best represents the following function?
Tap to reveal answer
The highest exponent of the variable term is two (
). This tells that this function is quadratic, meaning that it is a parabola.
The graph below will be the answer, as it shows a parabolic curve.
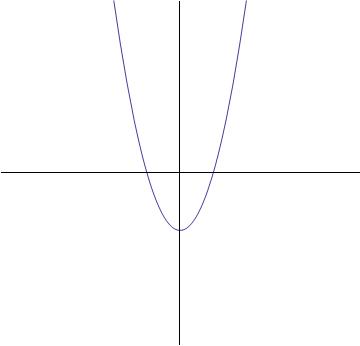
The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.
← Didn't Know|Knew It →
Tap to reveal answer
The function includes all possible y-values (outputs). There is nothing you can put in for y that won't work.
The function includes all possible y-values (outputs). There is nothing you can put in for y that won't work.
← Didn't Know|Knew It →
Tap to reveal answer
A number taken to a power must be positive.
A number taken to a power must be positive.
← Didn't Know|Knew It →
Tap to reveal answer
The square root of any number cannot be negative.
The square root of any number cannot be negative.
← Didn't Know|Knew It →
Tap to reveal answer
The absolute value of a number cannot be negative.
The absolute value of a number cannot be negative.
← Didn't Know|Knew It →
For the function 
, please state the end behavior, find any local maxima and local minima, and then state whether the graph symmetry is even, odd, or neither even nor odd.
For the function 
Tap to reveal answer
To get started on this problem, it helps to use a graphing calculator or other graphing tool to visualize the function. The graph of 
is below:
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Next, look at x=2, then x=3, and so on, and you can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 
and as 
.
Next, the question asks to identify any local minima and maxima. It helps to think of these as "peaks" and "valleys." Looking at the graph, it appears that these exist at the points (0, 1) and (2, -3). We can check this algebraically by plugging in these x values and seeing that the associated y values come out of the function.
This confirms that the point (0, 1) is a local maxima (peak) and the point (2, -3) is a local minima (valley).
Finally, the question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. The right side of this graph has a local minima, while the left side does not, therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does not, therefore, the graph has no symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x).
To get started on this problem, it helps to use a graphing calculator or other graphing tool to visualize the function. The graph of 
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Next, look at x=2, then x=3, and so on, and you can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 
Next, the question asks to identify any local minima and maxima. It helps to think of these as "peaks" and "valleys." Looking at the graph, it appears that these exist at the points (0, 1) and (2, -3). We can check this algebraically by plugging in these x values and seeing that the associated y values come out of the function.
This confirms that the point (0, 1) is a local maxima (peak) and the point (2, -3) is a local minima (valley).
Finally, the question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. The right side of this graph has a local minima, while the left side does not, therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does not, therefore, the graph has no symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x).
← Didn't Know|Knew It →
Below is the graph of 
Select the choice that correctly indicates this graph's end behavior.
Below is the graph of
Select the choice that correctly indicates this graph's end behavior.
Tap to reveal answer
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As and as .
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As
← Didn't Know|Knew It →
Below is the graph of 
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Tap to reveal answer
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph, while Quadrant II (x negative, y positive) has no part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph, while Quadrant II (x negative, y positive) has no part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
← Didn't Know|Knew It →
Below is the graph of 
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Tap to reveal answer
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. We can see that what is on the left side of the line x=0 is an exact match of what is on the right side of the line x=0. Therefore, this graph has even symmetry. Algebraically, a function has even symmetry if f(x)=f(-x). You can plug in several test values of x to see this for yourself.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. We can see that what is on the left side of the line x=0 is an exact match of what is on the right side of the line x=0. Therefore, this graph has even symmetry. Algebraically, a function has even symmetry if f(x)=f(-x). You can plug in several test values of x to see this for yourself.
← Didn't Know|Knew It →